Você sabe o que uma explosão nuclear, a análise do formato do seu crânio e um detector de bombas falso têm em comum com a análise sismográfica de desmontes para atender aos limites de vibração da NBR 9653:2018?
A frenologia, teoria pseudocientífica do século XIX, afirmava que era possível identificar inteligência, traços de personalidade e até tendências criminosas pelas saliências do crânio. Com mapas cranianos detalhados, linguagem técnica e instrumentos como o frenoscópio, ela seduziu médicos, juristas e empresários. Na prática, era uma forma de mascarar preconceitos sociais com verniz científico, oferecendo respostas simples para fenômenos complexos.
Mais de um século depois, o mundo veria algo semelhante com o ADE 651 — um “detector de bombas” vendido a governos por milhares de dólares. O equipamento, apresentado com jargão técnico e aparência sofisticada, era na verdade um bastão de plástico com uma antena móvel, ativada involuntariamente pelo pulso do operador. Seu uso levou à morte de centenas de pessoas em atentados que poderiam ter sido evitados.
Essas histórias nos lembram que modelos mal fundamentados, mesmo com aparência científica, podem trazer sérias consequências.
Mas o que tudo isso tem a ver com a vibração gerada por um desmonte? Mais do que limitar velocidades de partícula a certos valores numéricos, projetar desmontes para atender a a NBR 9653:2018 exige um entendimento um pouco mais profundo do que uma simples equação de previsão de velocidade de pico de partícula. Você precisa entender o que são as frequências de oscilação, por que elas importam e como elas afetam a resposta estrutural.
Neste texto, vamos construir, passo a passo — do sistema massa-mola amortecido à integral de Duhamel, da análise dimensional ao espectro de resposta — uma abordagem clássica para prever frequências e estimar as velocidades de partícula com modelos um pouco mais completos que os clássicos.
Nosso objetivo é mostrar que projetar desmontes conforme a NBR 9653:2018 não é simplesmente aplicar uma fórmula de previsão de PPV. É entender como uma estrutura vibra, por que vibra, e o que acontece quando ela encontra a frequência errada no momento errado.
E no final deste texto, retornaremos às histórias da frenologia e do ADE 651 — para mostrar como metáforas ruins, modelos mal escolhidos e interpretações frágeis podem gerar uma confiança perigosa.
Sir Taylor e a bomba.
Durante a Segunda Guerra Mundial, quando os testes nucleares do Projeto Manhattan ainda eram segredos de Estado, o físico inglês Sir Geoffrey Ingram Taylor surpreendeu o mundo ao estimar, com notável precisão, a energia liberada na explosão da bomba atômica — apenas observando fotografias da frente de choque em expansão publicadas em revistas populares.
Sem acesso a relatórios confidenciais, fórmulas mágicas ou sensores sofisticados, ele usou análise dimensional — uma ferramenta conceitualmente simples, mas poderosa. Particularmente, a grande estrela da análise feita por Taylor foi o Teorema \(\pi\) de Vaschy-Buckingham.
Uma pequena descrição deste teorema é necessária para que você possa trilhar nosso texto sem maiores dificuldades. Senão vejamos.
A natureza puramente física das coisas: nada depende de como nomeamos a massa, o comprimento ou o tempo. O Teorema \(\pi\) de forma simplificada.
As leis naturais não dependem das unidades que escolhemos. Seja qual for o sistema de medida — metros ou polegadas, segundos ou milênios, gramas ou toneladas — o comportamento da natureza permanece o mesmo. Naquela manhã bem fria de inverno, o acordar descalço e a topada do mindinho na quina da cama vai te causar a mesma dor se você medir a força aplicada no seu pobre dedinho em Newtons, Dinas ou qualquer outra unidade que queira.
Além disso, toda equação física precisa ser dimensionalmente coerente. Não dá pra somar metros com segundos nem igualar uma força com uma distância.
A partir dessas constatações surge o Teorema \(\pi\) de Vaschy-Buckingham, que diz basicamente o seguinte:
Se um fenômeno físico envolve \(n\) variáveis com \(k\) dimensões fundamentais (como massa, comprimento e tempo), então ele pode ser descrito por \( p = n−k \) combinações adimensionais, chamadas de \( \pi_1,\pi_2,…,\pi_p \), de modo que:
\( F(\pi_1, \pi_2, \dots, \pi_p) = 0\)
Eu sei, esse teorema parece meio estranho na primeira vez que você topa com ele. E se você se aprofundar mais, verá que ele é intimamente ligado a conceitos da algebra linear quando você trata as dimensões como vetores de uma base canonica e procura pelo espaço nulo da matriz associada as unidades do fenômeno estudado. Mas nós não vamos nos aprofundar nos detalhes deste teorema, não é o foco aqui.
A última parte é muito sintética – no sentido de trazer muito conteúdo em uma pequena dose:
\( F(\pi_1, \pi_2, \dots, \pi_p) = 0\)
Vamos tentar destrinchá-la melhor.
Primeiro, observe que \(F\) é uma notação para uma função.
Isso significa que \(F\) pega um monte de variáveis — no nosso caso, \(\pi_1,\pi_2\dots,\pi_p\) — e devolve um único valor como resposta. No caso do Teorema \(\pi\), esse valor é zero:
\( F(\pi_1, \pi_2, \dots, \pi_p) = 0\)
Pode parecer estranho uma função “devolver zero”, mas isso é comum na física. É igual quando você tem uma equação do tipo:
\( y = 2x + 1\rightarrow F(x,y) = y − 2x − 1 = 0 \)
Perceba que isso é a mesma coisa — só escrita de outro jeito.
E o que são, afinal, esses números \(\pi\)?
Eles são as combinações adimensionais que surgem a partir das variáveis envolvidas no problema físico que estamos estudando.
Pense neles como as unidades neutras do sistema: não importa se você mede em metros ou polegadas, segundos ou horas — o valor de um número \(\pi\) continua o mesmo. É como se ele representasse a essência do fenômeno, sem as amarras das unidades de medida.
Na maioria das introduções ao Teorema \(\pi\), o pessoal costuma usar o famoso número de Reynolds, aquele que aparece na dinâmica dos fluidos e decide se o escoamento é laminar ou turbulento. Mas isso exige mais tempo, envolve viscosidade e não ajuda muito no que queremos aqui.
Nosso foco não é o Teorema \(\pi\) em si (e, diga-se de passagem, acho que já passamos por uns bons parágrafos sobre ele). O que a gente realmente quer é entender como usar ideias simples de grandezas físicas, como o pessoal faz no estudo das vibrações por desmonte de rocha e assim como Sir Geoffrey Taylor deduziu a quantidade de energia de uma explosão nuclear.
Sir Taylor sabia que, idealmente, durante uma explosão como a de uma bomba atômica, forma-se uma onda de choque esférica que se propaga pelo ar. Essa onda carrega consigo grande parte da energia liberada pela explosão e comprime violentamente o ar à sua frente.
Taylor supôs que o raio \(R\) da frente da onda de choque dependeria apenas de três coisas:
- A energia \( E \) liberada na explosão;
- A densidade do ar \( \rho \) ;
- E o tempo \( t \) decorrido desde a detonação.
Em outras palavras, ele considerou que havia uma função do tipo:
\(R = f(E,\rho,t)\)
Mas ele não queria saber como era a função \(f\). Ele queria encontrar a forma geral dessa relação, e pra isso usou o Teorema \( \pi\) !
Veja, as variáveis envolvidas têm as seguintes dimensões:
- \(R \rightarrow [L]\)
- \(E \rightarrow [M L^2 T^{-2}]\)
- \(\rho \rightarrow [M L^{-3}]\)
- \(t \rightarrow [T]\)
Temos \(n=4\) variáveis, e elas envolvem \( k=3 \)dimensões fundamentais (massa, comprimento e tempo).
Logo, o Teorema \(\pi\) nos garante que existe apenas um número adimensional: \(p = n−k = (4 – 3) = 1\), e a ideia é montar uma combinação dessas variáveis que não tenha unidade nenhuma. Essa é a essência do Teorema \(\pi\).
Vamos tentar uma combinação geral do tipo:
\( \pi_1 =R^aE^b\rho^ct^d\)
Para continuar, fazemos algo bem simples: substituímos cada variável — \(R,E,\rho,t\) — pelas suas dimensões físicas. Lembre-se que essas dimensões envolvem apenas três unidades fundamentais:
- \(M\): massa
- \(L\): comprimento
- \(T\): tempo
Assim, nosso numero adimensional \(\pi_1\) pode ser reescrito:
\(
\pi_1 = R^aE^b\rho^ct^d = [L]^a[ML^2T^{−2}]^b[ML^{−3}]^c[T]^d
\)
Reagrupando as potencias de mesma base temos:
\(
[L]^{a+2b-3c}[M]^{b+c}[T]^{d−2b}
\)
Para que \(\pi_1\) seja adimensional, todos os expoentes devem ser zero, logo:
\(
a+2b-3c = 0\\
b+c = 0\\
d−2b = 0\\
\)
Agora é que você percebe que temos quatro variáveis – a,b,c,d- e três equações? Isso mesmo. É isso que o Teorema \(\pi\) nos disse: para o nosso caso, temos um número adimensional, ou seja, um grau de liberdade no nosso sistema. E isso, grosso modo, diz que você pode, impunemente, escolher qualquer valor para uma das variáveis que as outras vão se encaixar na sua escolha, naturalmente. Significa que o sistema tem uma solução livre, ou seja, podemos escolher um dos expoentes à vontade (por exemplo, \(b=1\)), e as demais variáveis serão determinadas a partir disso.
Vamos escolher \(b=1\). (Poderíamos escolher outro valor qualquer, mas isso só muda o “formato” da resposta, e não o conteúdo físico.)
Agora que temos:
- a=−5
- b=1
- c=−1
- d=2
Substituímos esses valores na expressão:
\(
\pi_1=R^aE^b\rho^ct^d=R^{−5}E^1\rho^{−1}t^2
\\
\pi_1=\frac{Et^2}{R^5\rho} = constante
\)
Taylor pegou fotos da explosão publicadas em revistas da época, nas quais o raio da frente de choque podia ser medido a partir de escalas visuais. Como o tempo \(t\) desde a detonação era conhecido, e a densidade do ar \(\rho\) também, ele pôde isolar \(E\) da equação:
\(
E=\frac{R^5\rho}{t^2}.A
\)
Para determinar a constante \(A\) que aparece na solução, Taylor se baseou nos trabalhos do físico soviético Leonid Sedov que, na mesma época, também estava estudando as equações da propagação de ondas de choque em meios compressíveis. Sedov chegou à mesma estrutura de solução de Taylor, só que com o modelo matemático completo.
A solução ficou conhecida como a solução de Taylor–Sedov (às vezes também chamada Taylor–von Neumann–Sedov), e a constante que aparece nessa fórmula depende do número de dimensões (2D ou 3D), das propriedades termodinâmicas do gás (como o índice adiabático), e das condições iniciais do modelo.
No caso da explosão atmosférica tridimensional, essa constante pode ser estimada como \(A \approx 1\), o que dá um bom chute inicial para a estimativa de \(E\). O resultado foi uma energia da ordem de:
\(E\approx 8\times10^{13} joules\)
que corresponde a cerca de 20 mil toneladas de TNT, muito próximo do valor real hoje conhecido para a bomba de Hiroshima.
Se você quiser se aprofundar na análise dimensional aplicada ao fenomeno do desmonte de rochas eu sugiro a leitura do livro Modelling the Effects of Blasting on Rock Breakage dos autores V.A. Borovikov e I.F. Vanyagin. Já te adianto: não é um livro, digamos, muito simples, requer uma certa base de matemática e física, mas garanto que vai te fazer bem, encarar uma leitura difícil é um bom exercício de crescimento. Este artigo G.I. Taylor and the Trinity test de Michael A.B. Deakin explica de maneira bem mais detalhada o desenvolvimento aplicado por Sir Taylor.
Em resumo, Sir Geoffrey Taylor mostrou que dá pra estimar a energia da explosão a partir de poucas variáveis — tempo, densidade do meio e raio da frente de choque — usando análise dimensional e o Teorema \(\pi\).
Mas a história não para por aí, o pessoal pegou o gancho e estendeu a análise para outros campos. Dois engenheiros, Nicholas Ambraseys e Robert A. Hendron Jr. são considerados “os caras” que levaram a análise dimensional para a previsão de vibrações de desmontes de rocha com uso de explosivos. Você pode encontrar muitas publicações destes dois gigantes da engenharia na base de dados da ISEE.
O teorema \(\pi\) e as vibrações no desmonte de rochas.
Ambraseys e Hendron consideraram os seguintes grupos de variáveis envolvidadas no estudo das vibrações geradas por cargas explosivas no desmonte de rocha:
Variáveis independentes (entrada do problema)
- \(E\): Energia do explosivo \([ML^2T^{−2}]\)
- \(R\): Distância da fonte ao ponto de medição \([L]\)
- \(\rho\): Densidade do meio \([ML^{−3}]\)
- \(c\): Velocidade de propagação da onda no meio \([LT^{−1}]\)
- \(t\): Tempo \([T]\)
Variáveis dependentes (resposta do sistema)
- \(u\): Deslocamento máximo de partícula \([L]\)
- \(v\): Velocidade máxima de partícula \([LT^{−1}]\)
- \(a\): Aceleração máxima de partícula \([LT^{−2}]\)
- \(f\): Frequência da vibração \([T^{−1}]\)
Aplicando o Teorema \(\pi\) a estes grupos de variáveis temos \(p = 9 – 3 = 6\) números adimensionais associados. Ou seja, é possível construir 6 números \(\pi_i\) que representam a essência do problema físico. Uma possibilidade de agrupamento é esta:
\(
\pi_1 = \frac{R^{3/2} \cdot \rho^{1/2} \cdot c}{E^{1/2}} \\
\pi_2 = \frac{E^{1/2} \cdot t}{R^{5/2} \cdot \rho^{1/2}} \\
\pi_3 = \frac{x}{R} \\
\pi_4 = \frac{v \cdot R^{3/2} \cdot \rho^{1/2}}{E^{1/2}} \\
\pi_5 = \frac{a \cdot R^4 \cdot \rho}{E} \\
\pi_6 = \frac{f \cdot R^{5/2} \cdot \rho^{1/2}}{E^{1/2}}
\)
Mas por que uma possibilidade de agrupamento? Existem outras? Sim! Poderíamos ter escolhido outras combinações que gerariam alguns outros números adimensionais – mas sempre limitado a 6 possíveis combinações unicas.
Os adimensionais clássicos que a galera usa são os que o Professor Charles Dowding apresenta – com muita mestria – no seu livro Blast Vibration Monitoring and Control (leitura obrigatória se você trabalha ou quer trabalhar com sismografia de uma maneira profissional). Os adimensionais são estes:
\(
\pi_1 = \frac{u}{R}\\
\pi_2 = \frac{v}{c}\\
\pi_3 = \frac{aR}{c^2}\\
\pi_4 = ft\\
\pi_5 = \frac{tc}{R}\\
\pi_6 = \frac{E}{\rho c^2 R^3}\\
\)
Uma escolha sábia faz parte da solução do problema. Veja que os parâmetros de \(\pi_1\) até \(\pi_4\) contem as variáveis dependentes e os dois últimos são combinações das variáveis independentes.
Com base no conjunto de adimensionais, é possível escrever a velocidade máxima da partícula como um produtório do tipo:
\(\frac{v}{c} = \prod_{n} \pi_n^{\alpha_n}\)
Essa equação geral é uma consequência direta do Teorema \(\pi\): ela nos diz que existe uma função que relaciona essas variáveis físicas através de números adimensionais — e que podemos expressar essa relação como um produto de potências de cada \(\pi\).
Mas aqui entra um ponto essencial da prática: Nem todos os termos do produtório têm o mesmo impacto sobre o fenômeno.
Dependendo do tipo de análise, da qualidade dos dados ou do nível de simplificação desejado, podemos manter apenas alguns poucos \(\pi_n\) — e considerar que os demais estão absorvidos no coeficiente a ser determinado empiricamente ou que variam pouco.
Assim, por exemplo, podemos escrever:
\(\frac{v}{c} = \pi_i^{\alpha_i} \cdot \pi_j^{\alpha_j} \cdot \dots\)
Selecionando apenas os \(\pi\) mais relevantes para o problema. O professor Dowding no seu livro, por exemplo, apresenta o seguinte modelo de previsão:
\(
u_{max} = 0,072 \left(\frac{30,5}{R}\right)^{1,1} \left(\frac{3050}{c}\right)^{1,4} \left(\frac{w}{4,54}\right)^{0,7} \left(\frac{2,4}{\rho}\right)^{0,7} (mm)
\\
v_{max} = 18,3 \left(\frac{30,5}{R}\right)^{1,46} \left(\frac{w}{4,54}\right)^{0,48} \left(\frac{2,4}{\rho}\right)^{0,48} (mm/s)
\\
a_{max} = 0,81 \left(\frac{30,5}{R}\right)^{1,84} \left(\frac{c}{3050}\right)^{1,45} \left(\frac{w}{4,54}\right)^{0,28} \left(\frac{2,4}{\rho}\right)^{0,28} (g)
\)
Perceba que estamos trabalhando com adimensionais puros, além disso observe dois fatores importantes:
1 – As equaçãoes são dimensionalmente corretas.
2 – O tempo não aparece por que são equações para a previsão dos valores máximos, não para toda a medição temporal dos valores de deslocamento, velocidade e aceleração de partícula.
Percebeu o uso do Teorema \(\pi\)? O problema é “precisamos estimar os valores máximos de deslocamento, velocidade e aceleração de partícula, quais as variáveis que entram no nosso estudo, ou seja, quais parametros físicos importam?”.
Dowding trabalhou com estes:
R – distância.
c – Velocidade de propagação do meio.
w – Carga explosiva.
\(\rho\) – Densidade do meio.
Além disso, utilizou valores de referência para cada variável e com isso, através de medições em campo, determinou os coeficientes para cada fator adimensional. Utilizar valores de referência significa que para o estudo em questão, se você estiver a uma distância de 30,5m da fonte, utilizar uma CME com 4,54kg de explosivos e estiver em um meio com densidade de 2,4 \(t/m^3\) terá uma velocidade de partícula de 18,3mm/s. E se os parametros forem outros? Então os expoentes de cada adimensional vaõ “calibar” seu resultado. Assim, estes valores de referencia apenas normalizam a equação em relação a um estudo inicial.
Existe outro modelo, talvez o mais amplamente conhecido e utilizado na prática, para a previsão da velocidade máxima de partícula:
\(
v_{max} = k \cdot \left( \frac{R}{Q^\beta} \right)^\alpha
\)
Note que, diferentemente das equações baseadas em números adimensionais, essa equação não é adimensional. O termo entre parênteses não é um número puro, e portanto o coeficiente ( k ) precisa carregar unidades para que a equação permaneça dimensionalmente correta.
Analisando as dimensões:
\(R \sim [L] \)
\(Q \sim [M] \)
Logo, o termo elevado a \( \alpha \) possui dimensão:
\(
\left( \frac{R}{Q^{\beta}} \right)^{\alpha} \sim [L]^{\alpha} \cdot [M]^{-\alpha \beta}
\)
Como sabemos que a dimensão de \( v_{max} \) é \( [L T^{-1}] \), o coeficiente ( k ) deve ter, obrigatoriamente, dimensão:
\( dim(k) = [L]^{(1 – \alpha)} \cdot [T]^{-1} \cdot [M]^{\alpha \beta} \)
Isso significa que o coeficiente \( k \) não é um número arbitrário: ele depende das unidades adotadas e dos valores dos expoentes utilizados. Essa dependência dimensional é frequentemente ignorada, o que pode gerar inconsistências ou dificultar a comparação entre diferentes modelos empíricos. Isso explica por que modelos ajustados com diferentes geometrias, maciços ou cargas explosivas apresentam coeficientes com diferentes magnitudes e unidades implícitas.
E importante observar que este modelo clássico pode ser compreendido — e até fundamentado — a partir de uma estrutura adimensional mais rigorosa. De fato, entre os números adimensionais extraídos por análise dimensional para o problema da vibração induzida por explosivos, temos:
\(
\pi_6 = \frac{E}{\rho c^2 R^3},
\)
Esse termo, além de ser adimensional, está relacionado à intensidade da frente de onda em uma propagação esférica. A teoria da propagação de ondas em meios elásticos mostra que a energia por área da frente de onda decresce com \( (1/R^{\gamma}) \), e que a velocidade de partícula associada é:
\(
v \sim \frac{1}{R^{\gamma}} \cdot \sqrt{\frac{E}{\rho c}},
\)
o que implica que o comportamento observado nos modelos empíricos, onde \( v \propto R^{-\alpha} \) com \( \alpha > 0 \), reflete diretamente essa atenuação geométrica natural da propagação da onda.
Portanto, ao se escrever:
\(
v_{max} = k \cdot \left( \frac{R}{Q^\beta} \right)^\alpha
\)
estamos, na prática, propondo uma relação empírica onde a distância atua como um fator de atenuação (por isso o expoente \( \alpha \) é negativo se reescrito como \( v \propto R^{-\alpha} )\), e o termo \( Q^\beta \) representa uma aproximação prática para a energia ( E ) — isto é, \( Q \propto E \).
Já vimos que esse modelo não é adimensional por si só, e por isso o coeficiente \( k \) precisa compensar as unidades físicas faltantes. Mas com o suporte da análise dimensional e da teoria da propagação de ondas, conseguimos entender a origem física dos expoentes e por que esse tipo de equação funciona tão bem em campo.
Mas por que todo esse desenvolvimento em torno de modelos de previsão de vibrações?
Porque, para projetar desmontes que possam atender aos limites de vibração da NBR 9653:2018, o modelo clássico isolado,
\(v_{max}=k \cdot \left( \frac{R}{Q^\beta} \right)^\alpha\)
é, na prática, inútil.
Esse modelo pode até prever com razoável precisão o valor máximo da velocidade de partícula, mas ele nada diz sobre as frequências do sinal gerado pela detonação. E a frequência é um parâmetro crítico, pois a NBR impõe limites de vibração que dependem das frequências geradas. Alem disso, a NBR9653 não trabalha com valores máximos de velocidade de particula, mas como todos os valores medidos nos intervalos de tempo. Portanto, prever \(v_{max}\) é completamente irrelevante para a NBR9653:2018
Ou seja, para saber se um desmonte respeita a norma é preciso estimar as frequências que podem ser geradas aliadas as suas respectivas velocidades de partícula.
Para isso, precisamos de modelos mais completos, como os apresentados por Dowding, que correlacionam:
- \(u_{max}\) — deslocamento máximo;
- \(v_{max}\) — velocidade máxima;
- \(a_{max}\) — aceleração máxima;
- E outros parâmetros físicos como \(c\), \(\rho\), \(R\), e a carga explosiva \(w\).
Mas antes de chegar à previsão da frequência principal, é fundamental compreender as hipóteses simplificadoras que nos permitem estimá-la. E o ponto de partida, universalmente aceito, é o modelo de um grau de liberdade amortecido: o clássico SDF Model (Single Degree of Freedom Model).
Sistema massa-mola amortecido com um grau de liberdade.
A figura abaixo introduz o conceito de um sistema massa-mola.
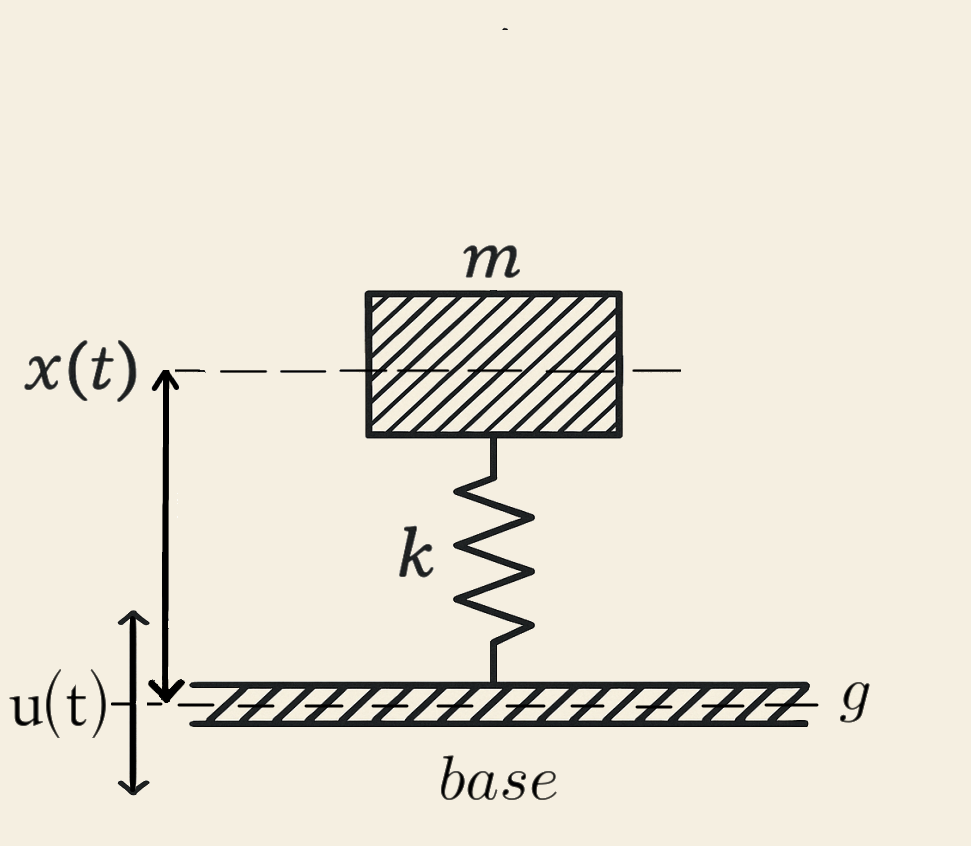
A mola, de constante \(k\), é o elemento que conecta a massa \(m\) à base. Inicialmente, a massa está em repouso em relação à linha de referência \(g\). Qualquer movimento relativo a essa linha é representado por uma função \(x(t)\). Na verdade, a linha \(g\) é a nossa referência fixa, isto é, a unica coisa que nãos e move nesse nosso modelo.
A base, por sua vez, também está inicialmente em repouso em relação a linha de referência \(g\). Qualquer movimento da base em relação a essa linha é descrito por uma função \(u(t)\).
Resumindo:
- x(t) representa o movimento vertical da massa em relação à linha de referência \(g\);
- u(t) representa o movimento vertical da base em relação à linha de referência \(g\).
A mola de constante \(k\) conecta a massa à base, e transmite forças elásticas entre elas.
Essa descrição representa um sistema idealizado: um sistema perfeito, que quando posto em movimento, nunca para. Isso acontece porque, nesse modelo com apenas uma mola e uma massa, a energia oscila continuamente entre forma cinética (na massa) e energia potencial elástica (na mola), sem perdas.
Concorde comigo: um sistema assim não tem muita chance de representar com fidelidade o comportamento de sistemas físicos reais. Precisamos inserir algo que “roube” um pouco da energia a cada ciclo de oscilação, dissipando-a, como acontece em qualquer sistema real.
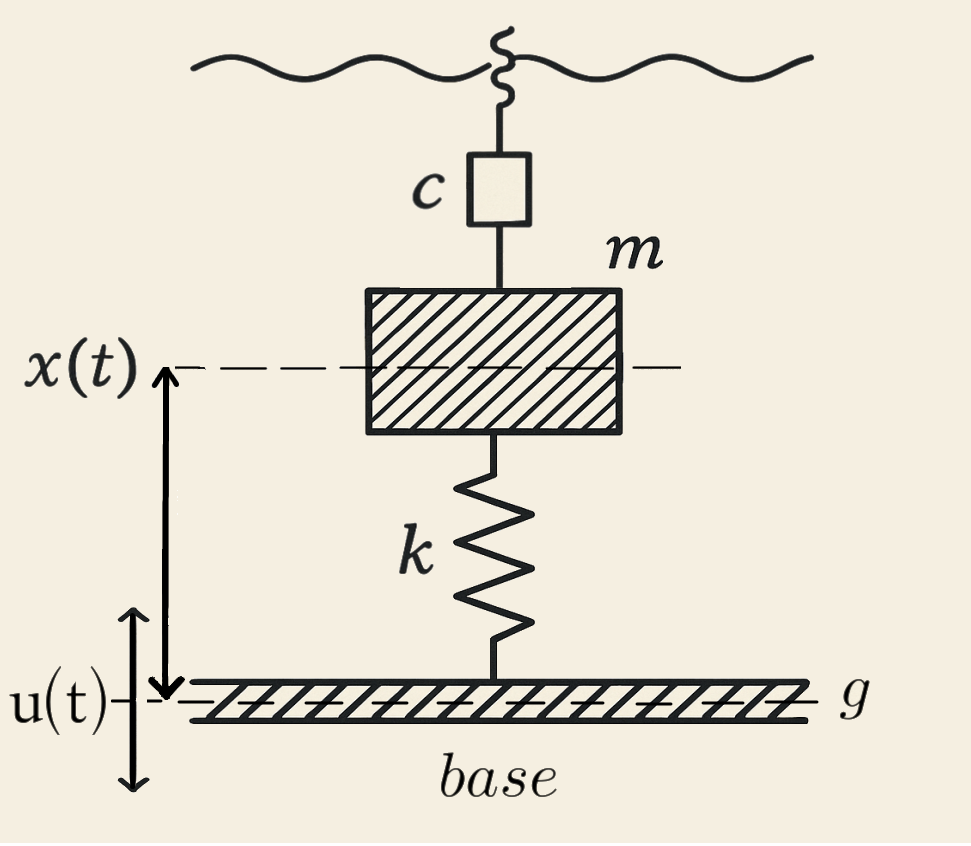
Para isso, introduzimos um amortecedor com coeficiente \(c\). Esse elemento representa tudo que consome energia sem armazená-la elasticamente — como atrito, resistência do ar, ou qualquer outro mecanismo dissipativo. O papel de \(c\) é justamente esse: consumir energia do sistema sem devolvê-la como movimento oscilatório, geralmente transformando-a em calor ou deformações permanentes.
A figura a seguir mostra a idealização deste sistema massa-mola com amortecimento — nosso modelo físico mais fiel ao comportamento real observado em estruturas e materiais sob excitação dinâmica.
Agora, vamos traduzir para uma linguagem mais universal todas estas considerações, vamos escrever este sistema segundo as Leis de Newton.
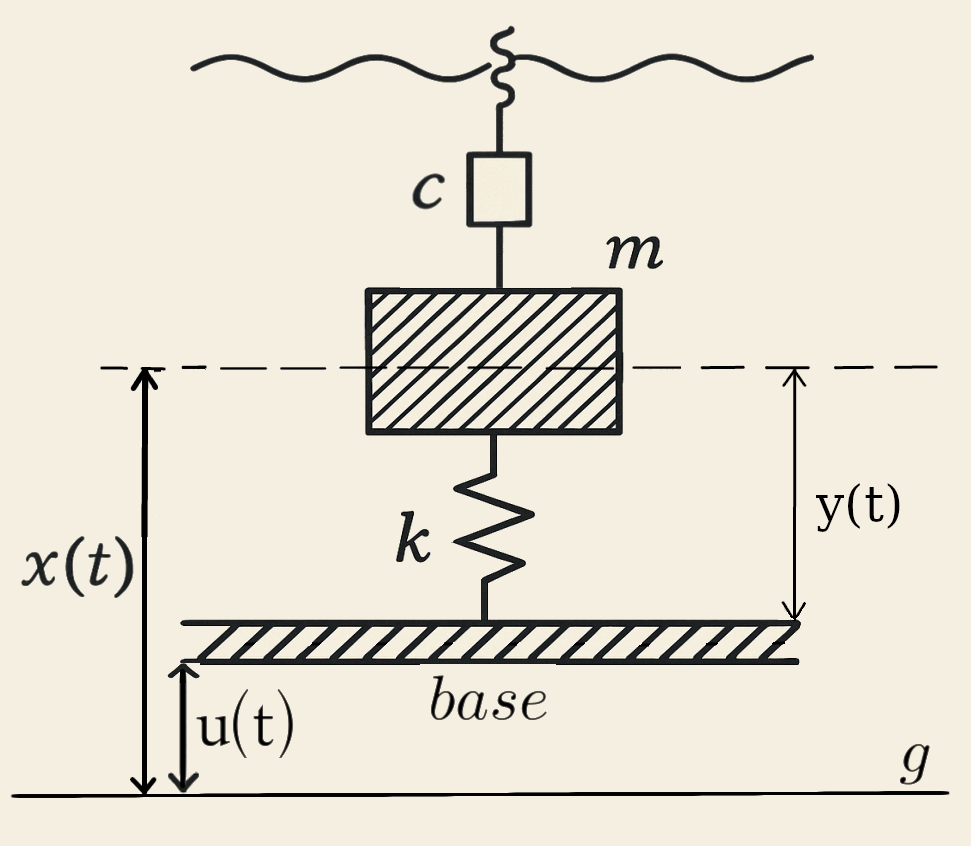
Observe que queremos resolver nosso sistema para o movimento relativo da massa em relação à base. Chamaremos a função que nos dá a posição da massa \(m\) em relação à base de \(y(t)\). E:
\(
y(t) = x(t)-u(t)
\)
É importante que você compreenda a função acima. Olhe a figra abaixo que mostra \(y(t)\) quando a base se desloca para cima da linha de referencia \(g\).
Aplicando a segunda Lei de Newton temos, de um lado da igualdade:
Força da mola: \(F_k=−k\cdot y(t) = −k (x(t)−u(t))\)
Força de amortecimento: \(F_c=−c \cdot \dot{y}(t) = −c(\dot{x}(t)−\dot{u}(t))\)
As força de amortecimento modelamos como sendo porporcional a velocidade da massa – assim como a força devido ao arrasto do ar devido a um corpo em queda livre. Desta fora os termos \(\dot{x}(t)\) e \(\dot{u}(t)\) são:
\(
\dot{x}(t)=\frac{dx}{dt}
\\
\dot{u}(t)=\frac{du}{dt}
\)
Tanto\(F_k\) quanto \(F_c\) possuem sinal negativo pois se opõem ao movimento da massa. Ambas resultam na força líquida agindo sobre \(m\), assim:
\(F_k + F_c = m\ddot{x}(t)\)
Perceba que \(\ddot{x}(t)\) é a aceleração da massa \(m\). Rearranjando os termos:
\(
m\ddot{x}(t) = F_k + F_c = -k(x(t) – u(t)) – c(\dot{x}(t) – \dot{u}(t))
\\.\\
m\ddot{x}(t) + c\dot{x}(t) + kx(t) = ku(t) + c\dot{u}(t)
\\.\\
\text{Como } y(t) = x(t) – u(t) \Rightarrow x(t) = y(t) + u(t)
\\.\\
m(\ddot{y}(t) + \ddot{u}(t)) + c(\dot{y}(t) + \dot{u}(t)) + k(y(t) + u(t)) = ku(t) + c\dot{u}(t)
\\.\\
m\ddot{y}(t) + m\ddot{u}(t) + c\dot{y}(t) + c\dot{u}(t) + ky(t) + ku(t) = ku(t) + c\dot{u}(t)
\\.\\
m\ddot{y}(t) + m\ddot{u}(t) + c\dot{y}(t) + ky(t) = 0
\\.\\
m\ddot{y}(t) + c\dot{y}(t) + ky(t) = -m\ddot{u}(t)
\)
Essa última equação mostra que o movimento relativo da massa depende diretamente de como a base é solicitada. E sim, você provavelmente já percebeu: estamos lidando com uma equação diferencial.
Isso significa, em termos simples, que não estamos procurando apenas um número, um valor específico da variável \(y(t)\), mas sim qual a forma que a função \(y(t)\) deve ter para que descreva o comportamento do sistema ao longo do tempo.
Se você se lembra das suas aulas de cálculo, deve recordar que, quando temos algo multiplicando a derivada de ordem dois — neste caso, a massa multiplicando a aceleração relativa: \(m\ddot{y}(t)\) — a resolução da equação se torna um pouco mais trabalhosa.
O melhor dos mundos, do ponto de vista da análise matemática, é deixar esse termo sozinho no lado esquerdo da equação, solitário como um estagiário no primeiro churrasco da obra. Para isso, basta dividir tudo pela massa \(m\):
\(
\frac{m\ddot{y}(t) + c\dot{y}(t) + ky(t)}{m} =\frac{ -m\ddot{u}(t)} {m}
\\.\\
\ddot{y}(t) + \frac{c}{m}\dot{y}(t) + \frac{k}{m}y(t) = -\ddot{u}(t)
\)
Agora aparecem dois coeficientes:
\(
\frac{c}{m}
\\
\text{e}
\\
\frac{k}{m}
\)
Esses dois coeficientes que surgem ao dividir a equação por \(m\) são como sal na cozinha: estão presentes em toda receita que envolve vibração. Vai encontrá-los em praticamente todo sistema oscilatório — seja numa ponte, numa máquina, em desmonte de rochas ou até no seu bolso, dentro do celular, quando ele vibra em uma chamada.
E são tão recorrentes que ganham nomes próprios:
- \( \frac{k}{m} \) é chamado de frequência natural ao quadrado, representado por \( (\omega_n)^2 \) (já veremos do porque “ao quadrado”);
- \( \frac{c}{m} \) está diretamente ligado à razão de amortecimento \( \xi \), uma grandeza adimensional que nos diz o quanto de energia o sistema dissipa a cada ciclo.
Para entender a frequência natural — \( \frac{k}{m} \) — vamos considerar a versão mais simples do nosso modelo: um sistema massa-mola sem amortecimento e sem excitação externa.
Eliminando o amortecimento \(c=0\) e supondo que a base não se move \(u(t)=0\), a equação de movimento relativa fica:
\(
m\ddot{y}(t)+ky(t) = 0 \rightarrow \ddot{y}(t)+\frac{k}{m}y(t)=0
\)
Essa é uma equação diferencial linear homogênea de segunda ordem com coeficiente constante. A solução geral depende das raízes da equação característica:
\(
r^2+\frac{k}{m}=0 \rightarrow r =\pm \imath \sqrt{\frac{k}{m}}
\)
Ou seja, a solução é oscilatória, do tipo:
\( y(t) =A \cos(\omega_nt)+B \sin(\omega_nt)\text{ com } \omega_n=\sqrt{\frac{k}{m}} \rightarrow \omega_n^2 = \frac{k}{m}\)
A constante \( \omega_n \) que aparece na solução é a frequência angular natural do sistema. Ela depende diretamente da rigidez da mola \(k\) e inversamente da massa \(m\).
Isso faz todo o sentido físico:
- Quanto mais rígido o sistema, mais rápido ele oscila;
- Quanto mais pesado, mais lento ele responde.
A frequência natural não é algo “inventado”: ela emerge naturalmente da solução da equação de movimento do sistema livre.
Ela é a característica mais fundamental de qualquer sistema oscilatório — o “batimento cardíaco” da estrutura. É dela que devemos nos distanciar quando falamos de frequencias associadas ao desmonte de rochas por explosivos. Se nosso desmonte gera frequências iguais ou muito próximas a frequencia natural da estrutura, a estrutura amplificará a sua resposta, ou seja, a velocidade de partícula medida na estrutura será maior que àquela que chegou até ela. Isto é um dos pilares teóricos do porque diversas normas de controle de vibração utilizam não só a velocidade de partícula como limitação mas também a frequencia associada.
Veja que, até certo ponto, o comportamento do sistema é definido por sua massa \(m\), por uma constante de mola \(k\) e por uma constante de amortecimento \(c\).
Quando estamos lidando com um modelo idealizado — como uma massa presa a uma mola — é relativamente simples identificar esses parâmetros. Mas e se, em vez de uma massa ideal, estivermos falando de um prédio de dez andares? Como medir a sua massa total? E pior ainda: o que seria a constante de mola \(k\) para uma construção desse tipo?
É nesse momento que a abstração puramente matemática começa a se distanciar da realidade prática da engenharia. Afinal, queremos usar esses modelos para analisar as oscilações reais de casas, prédios, pontes e estruturas em geral. Mas como traduzir a ideia de “constante de mola” para algo que faça sentido no mundo físico?
No modelo ideal, \(k\) mede a rigidez da mola: quanto mais difícil é comprimi-la, maior o valor de \(k\). Isso se traduz diretamente na fórmula da força elástica:
\(F=k \cdot \Delta x\)
Mas quando tratamos de construções reais, não existe uma mola visível ligando o edifício ao solo. Então, o que seria \(k\), nesse caso?
A resposta está na rigidez efetiva do sistema como um todo. Isso inclui:
- A rigidez dos materiais (concreto, aço, alvenaria);
- As condições de apoio e fundação;
- A distribuição de massa;
- E principalmente, a resposta global da estrutura à uma força lateral, como a provocada por uma detonação ou um terremoto.
Ou seja, \(k\) representa a capacidade da estrutura de resistir à deformação, como se ela fosse uma “mola distribuída”.
Ao invés de tentar medir \(k\), ou a massa, diretamente (o que seria quase impossível), recorremos a algo que podemos medir com ensaios ou sensores, desta forma nosso modelo matemático é reescrito de forma a utilizar parâmetros mais acessíveis e universais, como frequência de oscilação e taxa de atenuação. Vejamos como isso se dá.
Voltamos a nossa equação original, mas sem a aplicação de qualquer estimulo externo:
\(\ddot{y}(t)+\frac{c}{m}\dot{y}(t)+\frac{k}{m}y(t)=0\)
Essa equação diferencial é a chave para entendermos os diferentes comportamentos possíveis do sistema. O que muda de um comportamento para outro são os coeficientes que acompanham os termos — em especial, o termo \(\frac{c}{m}\).
A equação característica associada à nossa equação diferencial é:
\(r^2+\frac{c}{m}r+\frac{k}{m}=0\)
A natureza das raízes dessa equação — reais, complexas, iguais ou distintas — determina como o sistema vibra (ou não vibra) ao longo do tempo. Temos 4 casos distintos de acordo com as raízes da equação caracteristica:
Caso 1: Sistema puramente elástico sem amortecimento.
Se \(c=0\), temos:
\(r^2+\frac{k}{m}=0 \rightarrow r=\pm \imath \sqrt{\frac{k}{m}}\)
A solução da equação é:
\( y(t)=A\cos(\omega_n t)+B\sin(\omega_n t)\text{ ,com }\omega_n=\sqrt{\frac{k}{m}}\)
O sistema oscila indefinidamente com frequência natural \(\omega_n\). Não há perda de energia — é o modelo ideal, teórico, que serve como ponto de partida.
Caso 2: Sistema amortecido.
Para valores intermediários de \(c\), a equação característica tem raízes complexas com parte real negativa. A resposta do sistema é:
\(y(t) = e^{-\alpha t} \left( A \cos(\omega_d t) + B \sin(\omega_d t) \right)\)
Neste caso, o sistema ainda oscila, mas com amplitude decrescente — a energia vai sendo dissipada gradualmente. Este é o caso da maioria das estruturas.
Caso 3: Sistema criticamente amortecido.
Existe um valor específico de \(c\) que faz com que as raízes da equação sejam reais e iguais. Isso ocorre quando:
\(\left(\frac{c}{m}\right)^2 = 4\frac{k}{m} \quad \Rightarrow \quad c = 2 \sqrt{km}\)
Chamamos esse caso de amortecimento crítico. A resposta é:
\(y(t) = (A + Bt) e^{-\omega_n t}\)
O sistema não oscila, mas volta ao equilíbrio o mais rápido possível. Esse é o limite entre os sistemas que oscilam e os que não oscilam.
Caso 4: Sistema superamortecido.
Se \(c > 2\sqrt{km}\), o sistema é superamortecido. As raízes da equação, \(r_1 \text{ e } r_2\), são reais, distintas e negativas. O sistema não oscila, e sua resposta é:
\(y(t) = A e^{r_1 t} + B e^{r_2 t}, \quad r_1, r_2 < 0\)
Embora a oscilação seja completamente eliminada, o retorno ao equilíbrio é mais lento do que no caso crítico. Este é o caso dos amortecedores do seu carro, por exemplo.
Apenas um pequeno parenteses: você já deve saber, mas não custa lembrar, as constantes \(A\) e \(B\) que aparecem nas soluções acima são determinadas pelas condições iniciais e/ou de contorno associadas a modelagem da ED.
Razão de amortecimento – \(\xi\).
Diante desses diferentes regimes de amortecimento, surge a ideia de definir um único parâmetro que, de certa forma, nos diga o quão próximo estamos do amortecimento crítico. Esse parâmetro é a razão de amortecimento \(\xi\), definida como:
\(\xi = \frac{c}{2\sqrt{km}}\)
A boa notícia sobre esse parâmetro é que podemos estimá-lo em campo. Com alguns sismógrafos, é possível extrair o valor de \(\xi\) diretamente da resposta da estrutura, sem precisar medir nem \(c\), nem \(k\), nem \(m\), individualmente.
E se podemos determinar \(\xi\) em campo, o ideal é reescrever a equação de movimento usando \(\xi\) e a frequência natural \(\omega_n\), no lugar das constantes \(k\), \(m\) e \(c\). Para isso, basta observar as relações entre essas variáveis:
- Frequência natural angular: \(\omega_n = \sqrt{\frac{k}{m}} \quad \Rightarrow \quad \frac{k}{m} = \omega_n^2\)
- Razão de amortecimento: \(\xi = \frac{c}{2\sqrt{km}} = \frac{c}{2m\omega_n} \quad \Rightarrow \quad \frac{c}{m} = 2\xi\omega_n\)
Substituindo essas expressões na equação de movimento:
\(\ddot{y}(t) + 2\xi\omega_n \dot{y}(t) + \omega_n^2 y(t) = 0\)
Essa é a forma universal e compacta da equação de um sistema massa-mola amortecido — válida para qualquer combinação de massa, rigidez e amortecimento, desde que você conheça \(\omega_n\) e \(\xi\).
A equação característica, agora de roupa nova
Substituir os parâmetros físicos por \(\omega_n\) e \(\xi\) muda também a equação característica:
\(r^2 + 2\xi\omega_n r + \omega_n^2 = 0\)
As raízes dessa equação são:
\(r = -\xi \omega_n \pm \omega_n \sqrt{\xi^2 – 1}\)
Se \( 0 < \xi < 1\) , temos \(\xi^2 – 1 < 0\) , e a raiz é complexa conjugada. Isso significa que a resposta será oscilatória com amortecimento, o que corresponde à esmagadora maioria das estruturas civis — a menos que tenham sido projetadas com algum tipo de isolamento ou amortecimento especial.
Dessa forma de solução extraímos a chamada frequência de oscilação amortecida, definida como:
\(\omega_d = \omega_n \sqrt{1 – \xi^2} \quad \text{(para } 0 < \xi < 1 \text{)}\)
O que essa frequência nos diz?
A variável \(\omega_d\) nos mostra com que frequência o sistema irá oscilar de fato, levando em conta o efeito do amortecimento. Quando \(\xi = 1\), estamos exatamente no caso de amortecimento crítico — e o sistema não oscila: ele responde uma única vez e decai suavemente.
Mas quando \(0 < \xi < 1\), entramos no reino das oscilações amortecidas — que é o que mais interessa quando estamos analisando edifícios, casas, pontes e estruturas reais.
Nesse caso, as raízes da equação característica são:
\( r = -\xi\omega_n \pm i \omega_d \)
A parte real \( \xi \omega_n \) determina a taxa de decaimento da oscilação;
A parte imaginária \( \omega_d \) determina a frequência de oscilação.
Solução completa da EDO
A forma geral da solução da equação diferencial nesse caso é:
\(y(t) = e^{-\xi \omega_n t} \left( A \cos(\omega_d t) + B \sin(\omega_d t) \right)\)
Ou seja, uma oscilação harmônica multiplicada por uma envoltória exponencial decrescente — o clássico “sino amortecido” da engenharia.
Veja no gráfico abaixo como a resposta se comporta para diferentes valores de \(\xi\). Quanto menor o valor de \(\xi\), mais lenta é a perda de energia. Quando \(\xi = 1\), a oscilação desaparece. Isso mostra, visualmente, a transição entre os regimes vibratórios conforme discutido acima.
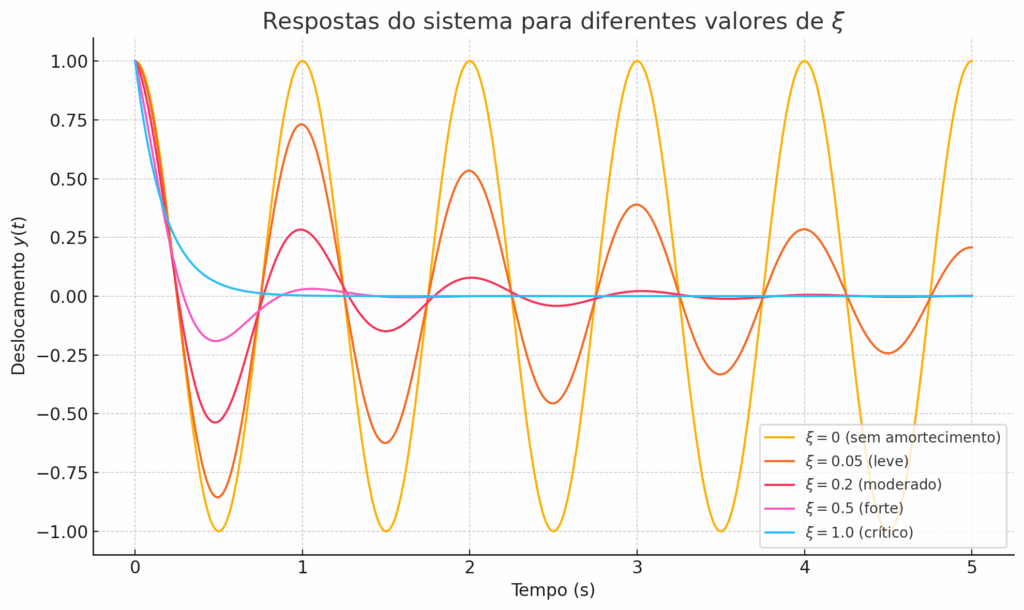
As estruturas que estamos acostumados a preservar quando efetuamos desmontes de rochas próximos a elas, diga-se: casas de um ou mais pavimentos, prédios, pontes, viadutos e outras similares possuem um coeficiente \(\xi\) entre \( 0,01 \leq \xi \leq 0,1\). Você pode utilizar esta faixa de valores para realizar simulações, mas saiba que é possível estimar o fator \(\xi\) medindo a resposta a oscilação de uma estrutura em particular. Se você está detonando próximo a uma edificação, por exemplo, pode medir a resposta dela – colocando o sismografo sobre ela, em diversos pontos – e utilizar uma técnica chamada de logaritmo decremental para extrair \(\xi\) diretamente do sismograma. Vejamos.
Estimando a razão de amortecimento com o logaritmo decremental
Imagine que o sistema é levemente amortecido (caso mais comum em estruturas reais). Quando você o excita e depois deixa vibrar livremente, ele começa a oscilar, mas com amplitude decrescente.
Essa resposta tem uma forma geral do tipo:
\(y(t) = A e^{-\xi \omega_n t} \cdot \cos(\omega_d t)\)
Se observarmos os valores de pico dessa resposta ao longo do tempo, perceberemos que eles descrevem uma curva exponencial decrescente. Isso porque a amplitude decresce como:
\(y_{\text{pico}}(t) = A e^{-\xi \omega_n t}\)
Veja no gráfico abaixo o que queremos dizer quando falamos em tomar dois valores de pico consecutivos.
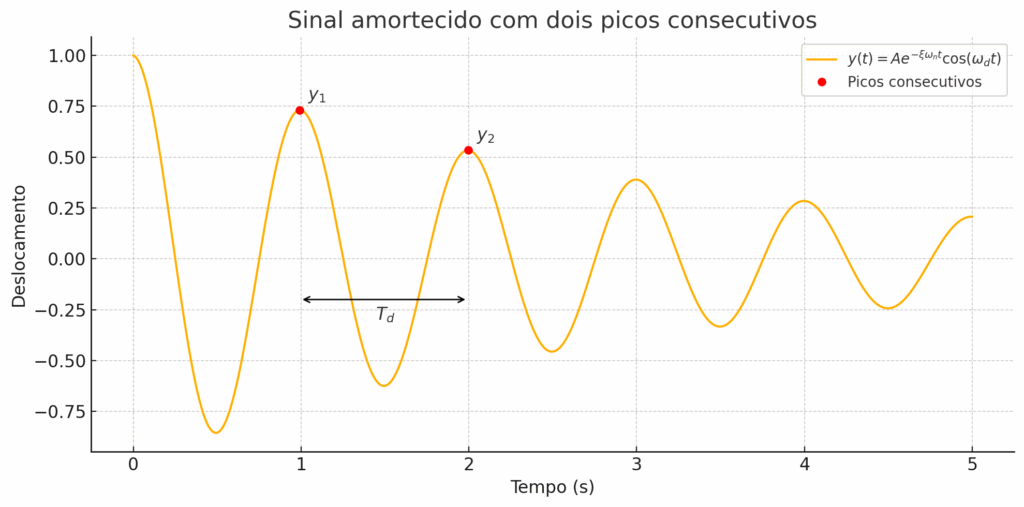
Onde estão os picos?
Os valores máximos (ou mínimos) da função ocorrem quando:
\(y_{\text{pico}}(t) = \pm A e^{-\xi \omega_n t}\)
Nesses instantes, a função \(y(t)\) atinge seus picos máximos e mínimos, que estão localizados sobre a envoltória exponencial:
\(y_{\text{pico}}(t) = \pm Ae^{−\xi\omega_nt}\)
Vamos considerar dois picos positivos consecutivos:
- \(y_1 = y(t_1)\)
- \(y_2 = y(t_2) \text{, com } t_2 = t_1 + T\)
Em que \(T\) é o período de oscilação, calculado localmente.
Um pequeno detalhe sobre este passo, que é importante: Até agora, temos nos referido a \(\omega_n\) e \(\omega_d\) como frequências angulares — ou seja, em unidades de rad/s. No entanto, para calcular o período da oscilação (em segundos), precisamos converter essas frequências para ciclos completos.
Isso é feito multiplicando por \(2\pi\), pois:
\(f_d = \frac{\omega_d}{2\pi} \quad \Rightarrow \quad T = \frac{1}{f_d} = \frac{2\pi}{\omega_d}\)
É importante deixar claro que estamos assumindo que a resposta do sistema segue a forma da solução da EDO — ou seja, uma oscilação senoidal amortecida. Isso é uma aproximação teórica.
Na realidade, o sinal medido por um sismógrafo contém uma miríade de frequências, modos estruturais e efeitos de dissipação não lineares. No entanto, sob certas condições, especialmente quando o sistema é bem comportado e a excitação não é muito caótica, essa aproximação senoidal ainda oferece excelente acurácia para os picos.
Essa hipótese é o que permite usar o logaritmo decremental como método confiável para estimar a razão de amortecimento \(\xi\).
Queremos agora observar como a amplitude decai de um pico para o próximo. Para isso, formamos a razão:
\(\frac{y_1}{y_2} = \frac{A e^{-\xi \omega_n t_1}}{A e^{-\xi \omega_n t_2}} = e^{\xi \omega_n (t_2 – t_1)}\)
Note que a constante \(A\) se cancela, e o que sobra é uma razão entre exponenciais.
Sabendo que \(t_2 – t_1 = T = \frac{2\pi}{\omega_d}\), temos
\(\frac{y_1}{y_2} = e^{\xi \omega_n T} = e^{\xi \omega_n \cdot \frac{2\pi}{\omega_d}}\)
Os valores \(y_1\) e \(y_2\) podem ser lidos diretamente no sismograma. Assim, se definimos a variável \(\delta\) como:
\( \delta = \ln\left(\frac{y_1}{y_2}\right)\)
E substituimos na expressão anterior:
\( \delta= \ln \left( e^{\xi\omega_n\frac{2\pi}{\omega_d} } \right) = \xi \omega_n\frac{2\pi}{\omega_d} \)
E finalmente, usando \(\omega_d = \omega_n \sqrt{1 – \xi^2}\), obtemos:
\( \delta = \frac{2\pi \xi}{\sqrt{1 – \xi^2} } \)
A variável \( \delta\) é conhecida como logaritmo decremental. Se isolamos \(\xi\) temos:
\( \xi = \frac{\delta}{\sqrt{4\pi^2 + \delta^2} } \)
Um pequeno exemplo. Veja no gráfico abaixo onde temos dois picos consecutivos \(y_1 \approx 0,5mm\) e \(y_2 \approx 0,4mm\)
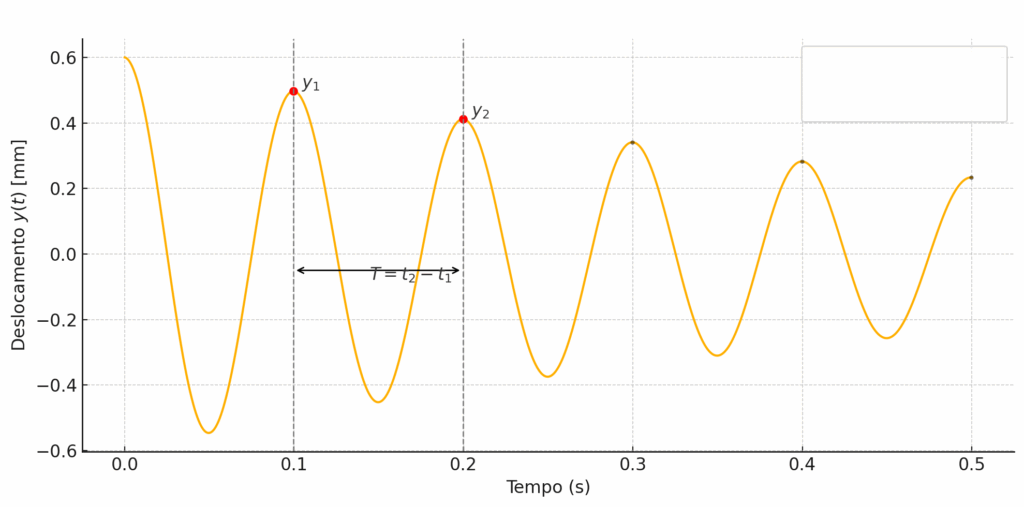
temos:
\(
\delta = \ln\left(\frac{0,5}{0,4}\right) \approx \ln(1,25)\approx 0,22
\\
\xi = \frac{0,22}{\sqrt{4\pi^2 + 0,22^2} } \approx \frac{0,22}{6,28}\approx 0,035 (3,5\%)\)
Até aqui, utilizamos a resposta de deslocamento de partícula \(y(t)\) para estimar a razão de amortecimento \(\xi\). Mas nada nos impede de aplicar o mesmo raciocínio usando a velocidade de partícula \(\dot{y}(t)\). Isso porque a envoltória exponencial não muda: ela está presente tanto no deslocamento quanto na velocidade, já que ambas derivam da mesma função base amortecida. A forma geral da velocidade é:
\(\dot{y}(t) = A e^{-\xi \omega_n t} \cdot f(t)\)
Onde \(f(t)\) é uma função oscilatória (cossenoides e senoides misturados), limitada entre +1 e -1, e os picos da velocidade ocorrem quando \(f(t) = \pm 1\). Assim, a envoltória da velocidade é:
\(\dot{y}_{\text{pico}}(t) \propto e^{-\xi \omega_n t}\)
Vamos considerar dois picos consecutivos de velocidade:
- Em \(t=t \text{, temos }\dot{y}_t = A e^{-\xi \omega_n t}\)
- Em \(t= t + T_d \text{, temos } \dot{y}_{t+1} = A e^{-\xi \omega_n (t + T_d)} = \dot{y}_t \cdot e^{-\xi \omega_n T_d}\)
Fazendo a razão:
\( \frac{\dot{y}_{t+1}}{\dot{y}_t} = e^{-\xi \omega_n T_d}\)
Aplicando o logaritmo:
\(\ln\left( \frac{\dot{y}_{t+1}}{\dot{y}_t} \right) = -\xi \omega_n T_d\)
Como o período de oscilação amortecido é:
\(T_d=\frac{2\pi}{\omega_n\sqrt{1-\xi^2}}\)
Temos:
\(
\delta_{\dot{y}} = -\xi \omega_n T_d
\\
\delta_{\dot{y}} = -\xi \frac{2\pi}{\sqrt{1-\xi^2}}
\\
\frac{\xi}{\sqrt{1-\xi^2}} = -\frac{\delta_{\dot{y}} }{2\pi}
\)
Se considerarmos estruturas civsis comuns, teremos um erro pequeno se considerarmos o termo \( 1-\xi^2 \approx 1\) para valores de \(\xi\) pequenos. Assim:
\(\xi \approx -\frac{\delta_{\dot{y}} }{2\pi}\)
E assim, você pode estimar \(\xi\) diretamente do seu sismograma de velocidade de partícula, quando o sismógrafo estiver medindo a resposta livre da estrutura após uma excitação — seja ela um desmonte, um impacto ou uma vibração induzida.
Na prática, você pode obter diversos valores de \(\xi\), dependendo do local da medição:
- Nos andares mais altos ou mais baixos;
- Próximo ao pé-direito ou sobre lajes;
- No centro ou nas bordas de um pavimento;
- Próximo a pilares ou sobre paredes.
Cada ponto da estrutura pode responder de forma ligeiramente diferente — e isso é perfeitamente normal. Afinal, a estrutura é tridimensional, contínua, com diferentes acoplamentos dinâmicos.
Nesse caso, você pode calcular o logaritmo decremental \(\delta\) em vários pontos e depois tirar a média:
\(\delta_{\text{medio}} = \frac{1}{n} \sum_{i=1}^{n} \ln\left( \frac{\dot{y}_{i}}{\dot{y}_{i+1}} \right)\)
E a partir disso, estimar um \(\xi\) médio:
\( \xi_{\text{médio}} = \frac{\delta_{ \text{medio} } } {2\pi} \)
Com uma única equação e dois picos consecutivos, você já tem um bom chute.
Com vários pontos e médias bem calculadas, você tem um modelo robusto e representativo do amortecimento real da sua estrutura.
O Espectro de Resposta, Pseudovelocidade e Pseudoaceleração
As deduções feitas até aqui — a solução da equação diferencial para o sistema amortecido, os parâmetros \(\omega_n\) e \(\xi\), e os modelos de previsão da velocidade de partícula baseados na análise dimensional — nos preparam para enfrentar dois desafios fundamentais da engenharia de explosivos:
- Prever como uma estrutura existente vai reagir dinamicamente a um evento de excitação — como um desmonte próximo;
- Estimar quais são as frequências principais que o seu desmonte irá gerar.
Antes de partirmos para essas deduções, precisamos abrir um pequeno parêntese para apresentar uma das ferramentas matemáticas mais importantes da resposta dinâmica: a solução da equação diferencial de um sistema amortecido via integral de Duhamel. Vamos lá.
A Integral de Duhamel — a resposta completa a qualquer excitação
Até agora, estudamos a resposta do sistema massa-mola-amortecido sem excitação externa — a chamada resposta livre.
Mas na prática, o que temos é sempre uma força que age sobre a estrutura ao longo do tempo, como vibrações causadas por:
- impactos;
- desmonte de rocha;
- tráfego;
- trens;
A equação de movimento com excitação externa, segundo tudo o que já desenvolvemos até agora, é:
\(\ddot{y}(t) + 2\xi\omega_n \dot{y}(t) + \omega_n^2 y(t) = \ddot{u}_g(t)\)
Nosso objetivo agora é encontrar a resposta \(y(t)\) para um dado sinal de excitação \(\ddot{u}_g(t)\). E quem resolve isso é a famosa integral de Duhamel.
A lógica é a seguinte: se a gente conhece a resposta do sistema a um impulso unitário (um “empurrãozinho” em \(t= \tau\)), então a resposta a qualquer \(\ddot{u}_g(t)\) pode ser construída como uma soma ponderada desses impulsos, cada um com sua força e seu momento de aplicação.
Em outras palavras:
A resposta total é a soma (integral) de infinitos impulsos multiplicados pela resposta que cada impulso gera.
Na física, a função matemática que podemos usar para representar um impulso, uma aplicação muito rápida de uma força (pense em uma raquete acertando a bola de tênis) é a famosa função Delta de Dirac denotada por \(\delta(t – \tau)\). Essa função tem duas propriedades fundamentais:
- Ela vale zero em todos os instantes, exceto no ponto \(t = \tau\);
- Sua integral em torno de \(\tau\) é igual a 1:
\(\int_{-\infty}^{\infty} \delta(t – \tau) \, dt = 1\)
Agora, o que fazemos é aplicar esse impulso ao sistema massa-mola-amortecido:
\(\ddot{y}(t) + 2\xi \omega_n \dot{y}(t) + \omega_n^2 y(t) = \delta(t – \tau)\)
A demonstração da solução da ED acima com a função impulso unitário como entrada é bem conhecida. Não vamos nos aprofundar aqui sob o risco de nos desviarmos demais do foco. A solução para condições iniciais nulas é:
\(h(t – \tau) = \frac{1}{m \omega_d} e^{-\xi \omega_n (t – \tau)} \sin(\omega_d (t – \tau)) \quad \text{para } t \geq \tau\)
e \(h(t – \tau) = 0\text{ para } t < \tau\).
Essa função \(h(t – \tau)\) é chamada de resposta ao impulso — ou função de Green — e representa como o sistema responde se for “cutucado” instantaneamente no tempo \(\tau\).
Agora, se sabemos como o sistema responde a uma “cutucada” e se assumimos que ele vai responder de maneira similar a muitas outras solicitações, então podemos somar (integrar) todas as respostas do sistema (todos os cutucões) e obter a solução geral:
\( y(t) = \int_0^t f(\tau) \cdot h(t – \tau) \, d\tau\)
Substituindo a função resposta \(h(t – \tau)\), obtemos a forma final da Integral de Duhamel:
\( y(t) = \frac{1}{m \omega_d} \int_0^t f(\tau) \cdot e^{-\xi \omega_n (t – \tau)} \cdot \sin(\omega_d (t – \tau)) \, d\tau \)
Se o carregamento for inercial, como no caso de vibração da base devido a um desmonte, temos:
\(f(t) = -m \ddot{u}_g(t) \quad \Rightarrow \quad y(t) = -\frac{1}{\omega_d} \int_0^t \ddot{u}_g(\tau) \cdot e^{-\xi \omega_n (t – \tau)} \cdot \sin(\omega_d (t – \tau)) \, d\tau\)
Onde:
- \(\ddot{u}_g(\tau)\): excitação aplicada na base no instante \(\tau\);
- \(y(t)\) como o sistema oscila em relação a base (lembre-se deste detalhe).
- \(\xi\): razão de amortecimento;
- \(\omega_n\): frequência natural;
- \(\omega_d =\omega_n\sqrt{1−\xi^2}\): frequência amortecida;
- O sinal negativo indica que o sistema tende a se mover em oposição à aceleração da base (efeito de inércia).
A integral de Duhamel mostra que:
- Cada pedacinho de força aplicado em um instante \(\tau\) provoca uma resposta oscilatória amortecida,
- A resposta é mais forte se o instante está mais próximo de \(t\), pois a exponencial decai com o tempo,
- A resposta total é a superposição (integração) de todas essas contribuições.
Essas considerações são, aliás, muito semelhantes ao que acontece em um desmonte, quando detonamos as cargas espaçadas no tempo, cada uma gerando sua parcela de energia vibratória.
Se você observar bem, estamos integrando em relação à aceleração da base \(\ddot{u}_g(t)\).
No entanto, nos nossos desmontes de rocha utilizamos sismógrafos com sensores de velocidade de partícula — os famosos LVTs (Low Velocity Transducers). Eles não medem diretamente a aceleração, e sim \(\dot{u}_g(t)\), a velocidade da partícula.
Além disso, a esmagadora maioria das normas de controle de vibrações e estudos de potencial de dano correlacionam esse risco diretamente com a velocidade de partícula. Por isso, seria extremamente útil ter a forma da Integral de Duhamel com o sinal de entrada como a velocidade.
Para isso, aplicamos integração por partes na forma clássica da integral de Duhamel. Se quiser os detalhes dessa dedução, recomendo uma referência essencial:
Veletsos, A.S. & Newmark, N.M. (1964)
“Design Procedures for Shock Isolation Systems of Underground Protective Structures, Volume III; Response Spectra of Single Degree of Freedom Elastic and Inelastic Systems”,
Air Force Weapons Laboratory Technical Documentary Report RTD TDR-63-3096 AD44989 – Volume III.
A forma resultante da integral é:
\(y(t) = -\int_0^t \dot{u}_g(\tau) \cdot e^{-\xi \omega_n (t – \tau)} \left[ \cos(\omega_d (t – \tau)) – \frac{\xi}{\sqrt{1 – \xi^2}} \sin(\omega_d (t – \tau)) \right] d\tau\)
Alguns detalhes importantes:
- A Integral de Duhamel agora trabalha com o sinal real que você mediu: a velocidade da partícula \(\dot{u}_g(t)\).
- Esse termo — \(\dot{u}_g(t)\) — representa todas as medições feitas a cada instante durante a oscilação da estrutura.
- E o mais importante: não importa se você usa aceleração \(\ddot{u}_g(t)\) ou velocidade \(\dot{u}_g(t)\) — o resultado da integral será sempre o deslocamento relativo \(y(t)\) da estrutura em relação à base.
Agora, a grande pergunta é: Que resultados úteis e práticos podemos extrair da integral de Duhamel?
A forma integral que desenvolvemos até aqui, seja com aceleração \(\ddot{u}_g(t)\) ou com velocidade \(\dot{u}_g(t)\), nos permite extrair duas grandes previsões práticas para a engenharia de vibrações causadas por desmontes de rocha:
- As chamadas pseudovelocidade e pseudoaceleração — duas grandezas derivadas que condensam, de forma elegante, a resposta máxima do sistema a uma excitação qualquer;
- O famosíssimo espectro de resposta, que nos mostra como diferentes sistemas reagem ao mesmo sinal, permitindo prever quais frequências estão sendo mais “energizadas” pelo desmonte.
Começaremos pela turma das “pseudo”.
Pseudovelocidade e Pseudoaceleração
Esses nomes podem parecer exóticos à primeira vista, mas o conceito por trás deles é simples e extremamente útil:
A pseudovelocidade é a velocidade equivalente que um sistema vibratório amortecido atingiria, caso fosse submetido à excitação registrada no solo.
Ela está associada diretamente ao deslocamento relativo máximo da estrutura em relação à base — ou seja, ao resultado \(y(t)\) que calculamos com Duhamel. Simplificando, você pega todo o seu sinal medido, no caso \(\dot{u}_g(t)\), e aplica na integral de Duhamel. Imagine que você tem \(n\) medições de velocidade de partícula, cada n-ésima medição serve de entrada \(\dot{u}(t_n)\) no integrando. Logo, cada entrada de velocidade vai gerar uma resposta de deslocamento. O maior valor de deslocamento \(y(t)\) que a integral retonar será utilizado para calcular a pseudovelocidade a pseudoaceleração.
Mas existem algumas hipóteses e considerações que devem ser aceitas:
- Você deve assumir que a oscilação pode ser razoavelmente aproximada por uma oscilação senoidal. Isso é bastante comum em vibrações estruturais, e nos permite usar as relações clássicas entre deslocamento, velocidade e aceleração, assumindo: \(y(t) = Y \cos(\omega t + \phi)\)
- Veja que existem pseudovelocidades e pseudoacelarações para cada par frequencia natural \(\omega_n\) e razão de amortecimento \(\xi\).
As clássicas relações entre deslocamento,velocidade,aceleração e frequência quando assumimos que o movimento é senoidal são:
- Velocidade: \(\dot{y}(t) = -Y \omega_n \sin(\omega_n t) \quad \Rightarrow \quad |\dot{y}_{\text{max}}| = \omega_n Y\)
- Aceleração: \(\ddot{y}(t) = -Y \omega_n^2 \cos(\omega_n t) \quad \Rightarrow \quad |\ddot{y}_{\text{max}}| = \omega_n^2 Y\)
E com isso, podemos agora definir:
- Pseudovelocidade: \(PV = \omega_n \cdot y_{\text{max} } \)
- Pseudoaceleração: \(PA = \omega_n^2 \cdot y_{\text{max} }\)
Se você está pensando que o maior valor medido da velocidade \(\dot{u}(t)\) vai produzir a maior pseudoaceleração, você não está totalmente certo. Veja, pode coincidir que a maior velocidade produza a maior pseudovelocidade de resposta. Mas nem sempre, ou melhor, quase sempre não é isso o que acontece.A integral de Duhamel mostra como um sistema determinado por uma frequencia natural \(\omega_n\) e uma razão de amortecimento \(\xi\) reaje a uma entrada qualquer e o valor máximo que ela retorna depende não só da entrada \(\dot{u}(t)\), mas também de \(\omega_n\) e \(\xi\) e de todo o passado do sinal. Vejamos um exemplo de como aplicamos Duhamel a um sinal discreto, igual aquele que você capta em campo com seu sismógrafo.
Então, nós temos sinal real, medido com um sismógrafo, na forma:
\(\dot{u}[t] = \left\{ \dot{u}_0, \dot{u}_1, \dot{u}_2, \dots, \dot{u}_N \right\}\)
ou seja, a velocidade de partícula medida ponto a ponto no tempo, com um intervalo de amostragem \(\Delta t\) entre cada valor. A maioria dos bons fabricantes de sismógrafos de engenharia, como White, Geosonics, Instantel, Vibracord, permitem exportar estes valores para cada canal. Ou seja, você pode obter as tabelas com velocidade x tempo para os canais longitudinal, transversal e vertical. E aqui fica a dica, utilize sismografos que te permitam obter os dados crus das medições. Assim você pode fazer as suas análises, independente da caixa preta dos softwares dos fabricantes.
Nosso objetivo é calcular a resposta relativa \(y(t)\) de um sistema definido por uma frequência natural \(\omega_n\) e razão de amortecimento \(\xi\) que foi, digamos, “chacoalhado” por esse sinal.
Conforme deduzimos acima, a versão da integral de Duhamel que trabalha com velocidade de partícula é:
\(y(t) = -\int_0^t \dot{u}_g(\tau) \cdot K(t – \tau) \, d\tau\)
Sim, eu sei, está um pouco diferente do que deduzimos acima. Mas é que eu separei o que chamamos de núcleo de convolução, para deixar tudo um pouco menos poluído e mais didático. O núcleo de convolução é:
\(K(t – \tau) = e^{-\xi \omega_n (t – \tau)} \left[ \cos(\omega_d (t – \tau)) – \frac{\xi}{\sqrt{1 – \xi^2}} \sin(\omega_d (t – \tau)) \right]\)
Veja que se você juntar tudo, retornamos a dedução feita anteriormente.
Como temos os dados em forma de um vetor discreto, isto transforma a integral em uma soma ponderada (também podemos chamar de convolução discreta):
\( y[n] = -\Delta t \sum_{k=0}^{n} \dot{u}[k] \cdot K[n – k] \)
Ou seja, para calcular o valor de \(y[n]\) (resposta no instante \(t_n = n \Delta t\):
- Percorra todos os valores passados de \(\dot{u}[k]\), de \(k=0\) até \(k = n\);
- Para cada valor \(\dot{u}[k]\), calcule quanto ele contribui com um peso \(K[n – k]\);
- Multiplique e some tudo;
- Multiplique o resultado final por \(-\Delta t\).
Percebeu que o núcleo \(K[n – k]\) é o coração da Duhamel?
Esse termo muda a cada \(n\) — e é isso que dá memória e seletividade de frequência ao sistema. Ele é calculado assim:
\(K[n – k] = e^{-\xi \omega_n (n – k)\Delta t} \left[ \cos(\omega_d (n – k) \Delta t) – \frac{\xi}{\sqrt{1 – \xi^2}} \sin(\omega_d (n – k) \Delta t) \right]\)
Ao final, você terá um vetor \(y[n]\) que representa a resposta relativa de uma estrutura com frequência \(\omega_n\) e amortecimento \(\xi\) ao sinal \(\dot{u}[t]\).
O maior valor de \(y[n]\) (ou seja, o máximo deslocamento relativo) é então usado para calcular a turma das pseudo:
- Pseudovelocidade: \(PV = \omega_n \cdot y[n]_{\text{max} } \)
- Pseudoaceleração: \(PA = \omega_n^2 \cdot y[n]_{\text{max} }\)
Vamos fazer um exemplo para fixar isso tudo. Temos o seguinte sismograma:
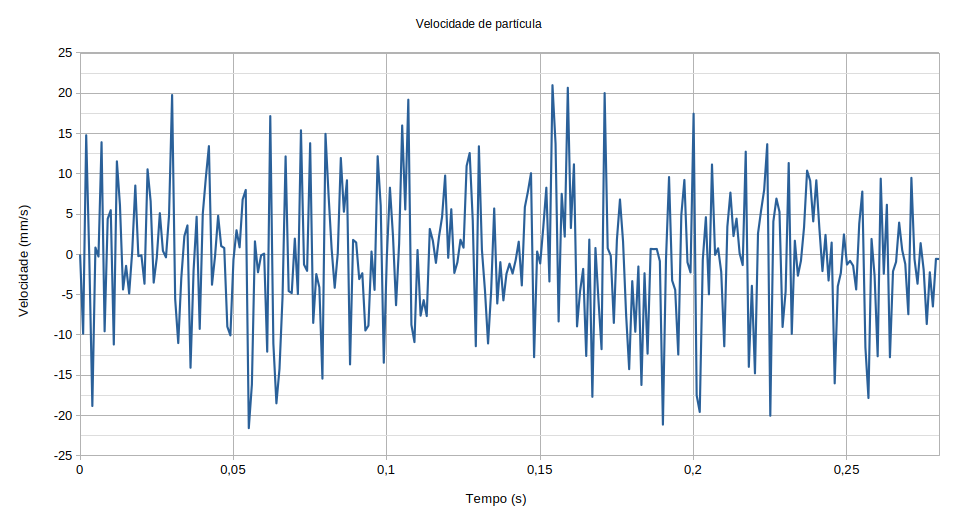
Parte da tabela associada ao gráfico acima é esta:
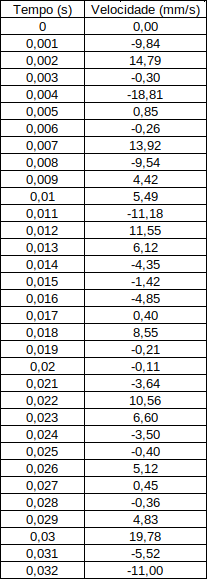
O código abaixo, escrito em Python, lê um arquivo contendo dois valores por linha, separados por tabulação e vírgula com separador de decimal (você pode ajustar ao seu tipo de formatação facilmente). Cada par de valores das linhas do arquivo corresponde ao dados da tabela acima, ou seja, são os números que dão origem ao gráfico do sismograma mostrado na figura acima.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("testeDuhamel.txt", sep='\t', header=None, decimal=',')
df.columns = ['tempo', 'velocidade']
# Parâmetros do sistema
xi = 0.03 # 3%
f_n = 10 # Hz
omega_n = 2 * np.pi * f_n
omega_d = omega_n * np.sqrt(1 - xi**2)
# Extrair dados
v = df['velocidade'].values # mm/s
t = df['tempo'].values # s
delta_t = np.mean(np.diff(t)) # intervalo de amostragem
# Criar núcleo de convolução K[n - k]
n = len(v)
K = np.zeros(n)
for i in range(n):
tau = i * delta_t
K[i] = np.exp(-xi * omega_n * tau) * (
np.cos(omega_d * tau) - (xi / np.sqrt(1 - xi**2)) * np.sin(omega_d * tau)
)
# Convolução discreta
y = -delta_t * np.convolve(v, K, mode='full')[:n]
# Gerar gráfico
plt.figure(figsize=(10, 5))
plt.plot(t, y, label='Resposta relativa $y(t)$')
plt.title("Resposta pela Integral de Duhamel")
plt.xlabel("Tempo (s)")
plt.ylabel("Deslocamento relativo $y(t)$ [mm]")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
# Valores máximos úteis
y_max = np.max(np.abs(y))
v_pseudo = omega_n * y_max
a_pseudo = omega_n**2 * y_max
print(f"Deslocamento relativo máximo (y_max): {y_max:.3f} mm")
print(f"Pseudovelocidade (v_pseudo): {v_pseudo:.3f} mm/s")
print(f"Pseudoaceleração (a_pseudo): {a_pseudo:.3f} mm/s²")Em uma primeira aplicação, rodaamos o código para uma razão de amortecimento de \(3\%\) e uma frequencia natural de oscilação de \(10Hz\). Os resultados foram estes:
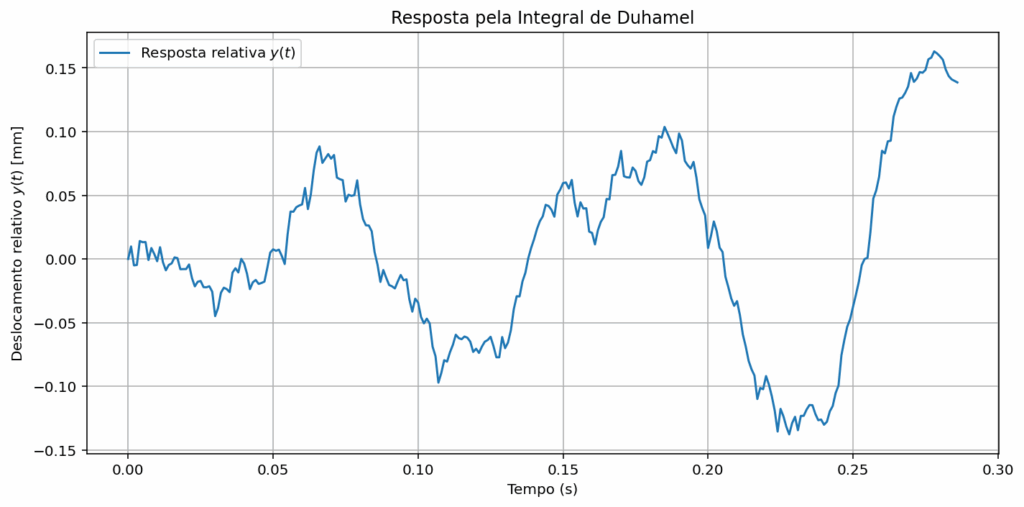
Deslocamento relativo máximo (y_max): 0.163 mm
Pseudovelocidade (v_pseudo): 10.241 mm/s
Pseudoaceleração (a_pseudo): 643.491 mm/s²
Veja, de acordo com nosso sismograma o maior valor de velocidade de partícula que atinge a estrutura é de 21,56mm/s. Mas a estrutura vai responder, no máximo, com 10,241mm/s. Isso porque nosso desmonte tem frequências bem distantes da frequencia de oscilação natural da estrutura, na verdade, nosso desmonte representando pelo sismograma tem frequências dominantes da ordem de 150 Hz a 200 Hz, se você aplicar uma FFT ao sinal vai encontrar estes valores.
A tabela abaixo mostra o mesmo sismograma para diferentes fequências naturais, mantendo a mesma razão de amortecimento de 3%:
| Frequencia natural (Hz) | Deslocamento máximo (mm) | Pseudovelocidade (mm/s) | Pseudoaceleração (mm/s²) |
| 4 | 0,103 | 2,579 | 64,824 |
| 5 | 0,114 | 3,587 | 112,685 |
| 10 | 0,163 | 10,241 | 643,491 |
| 15 | 0,163 | 15,377 | 1449,21 |
| 20 | 0,08 | 10,026 | 1259,91 |
| 30 | 0,115 | 21,71 | 4092,248 |
| 40 | 0,117 | 29,366 | 7380,364 |
| 50 | 0,087 | 27,315 | 8581,37 |
| 70 | 0,098 | 43,188 | 18994,983 |
| 100 | 0,07 | 43,796 | 27517,77 |
| 150 | 0,063 | 58,973 | 55580,543 |
| 200 | 0,069 | 86,364 | 108528,066 |
Percebeu que, conforme a frequencia natural do sistema aumenta, a resposta também aumenta, ou seja, a velocidade de partícula da estrutura aumenta? Para frequencias naturais baixas, em torno de 5 Hz a 20 Hz, como nosso desmonte possui frequencias dominantes muito altas a estrutura responde atenuando as vibrações. Mas, se por acaso a estrutura tivesse uma frequencia natural de oscilação muito mais alta, dentro do intervalo [150 Hz ; 200 Hz] então ela amplificaria muito o sinal, ou seja, entraria em ressonância. Percebe agora por que a NBR 9653 utiliza como limite, também, a frequência e não somente a velocidade de partícula?
Veja na animação abaixo como é a resposta via Duhamel quando vamos aumentando a frequência natural, deixando ela cada vez mais próxima das frequências dominantes do nosso desmonte.

Veja que quando as frequencias naturais de oscilação das estruturas se aproximam das frequências dominantes do nosso desmonte fenômenos como ressonância e batimentos ocorrem. Isso significa que a estrutura amplifica o sinal (vibração). E isso é ruim, não queremos isso.
Até agora lidamos com um sismograma pronto, um evento captado e analisamos como este evento provoca estruturas com coeficiente de amortecimento da ordem de 3% e com algumas frequencias naturais de oscilação. Mas, e se queremos, de alguma forma, saber quais as possíveis frequências que nosso desmonte vai gerar antes de detonar? De certa forma dá para fazer isso, mas conseguimos ir até alguns limites onde as hipóteses que devem ser feitas começam a não sustentar mais a realidade, ou seja, é possível mas você deve tomar alguns cuidados. Vejamos.
Definição da frequência principal e frequências dominantes.
As considerações e hipóteses que devem ser aceitas para estimar as frequências principais e dominantes do seu desmonte são estas:
- Suas medições devem poder sofrer uma aproximação senoidal sem maiores prejuízos, isto é, o sinal gravado pelo sismografo pode ser aproximado por uma senoide.
- O item acima, geralmente, só pode ser considerado quando estamos proximos ao desmonte e/ou o meio de propagação possui um homegeniedade adequada. Meios muito heterogênios ou distâncias muito grandes, transformam o sinal em um modelo aleatório, com diversas frequências presentes e com o mesmo peso para a amplitude. Isso dificulta, e muito, a aproximação senoidal. Mas não há uma receita que eu possa lhe dizer de quanto seriam estas distâncias ou quais seriam exatamente os meios ideiais.
- Se podemos usar uma aproximação senoidal sem maiores problemas, então as frequências teóricas geradas pelo sequenciamento do seu desmonte devem estar inclusas dentro do intervalo de previsão das frequências dominantes. Isso pode não ser tão simples de se fazer. Dependendo da configuração do seu desmonte, pode ser necessário delegar a previsão de frequências para mais do que um só modelo matemático.
- Para prever as frequências dominantes é necessário um modelo mais robusto que possa prever tanto os valores máximos como mínimos prováveis para o deslocamento, velocidade e aceleração de partícula.
Este último ítem é condição sine qua non. O que queremos dizer com isso é que, tavez tudo bem se as outras condições não forem tão perfeitas assim, mas se você não tiver um modelo que faça a previsão de das três variáveis citadas, você não vai conseguir prever frequência alguma. Não com a aproximação senoidal, pelo menos.
Existe uma técnica muito usada pela galera da dinâmica estrutural e do pessoal que trabalha com sismologia que é a do tripartite paper, ou gráfico tripartido, em uma tradução livre. Basicamente, você plota os valores das pseudovelocidades, pseudoacelerações e deslocamento máximo em um gráfico que é feito desta forma:
- O eixo horizontal contem as frequencias.
- O eixo vertical, as pseudovelocidades.
- Os eixos isometricos da aceleração partem a 45 graus do eixo horizontal.
- Os eixos isometricos do deslocamento partem a 135 graus do eixo horizontal.
Abaixo um exemplo da utilização desta técnica.

Author: Duku, Pendo M, Fugro WestStewart, Jonathan P, University of California, Los AngelesWhang, Daniel H, ExponentVenugopal, Ravi, Sysendes
Available from: https://www.researchgate.net/publication/245403651_Digitally_Controlled_Simple_Shear_Apparatus_for_Dynamic_Soil_Testing
Segundo Dowding, as frequencias dominantes do seu desmonte estarão presentes entre o limite inferior, dado pelo deslocamento, e o limite superior, dado pela aceleração. Veja na figura abaixo o local destacado em vermelho.
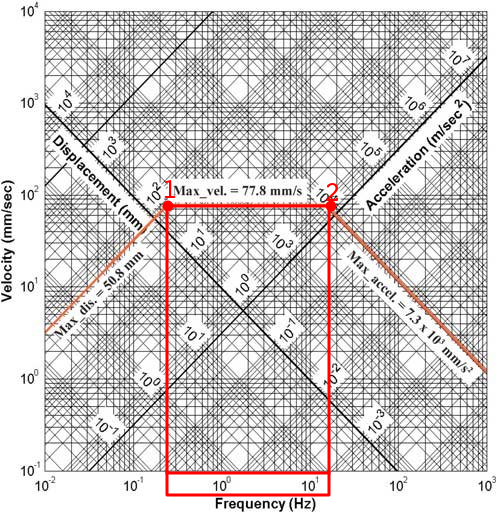
Veja que só é possível encontrar os vértices máximos no gráfico se você tiver três modelos de previsão, conforme mostramos no inicio deste texto quando mostramos o modelo adotado pelo professor Dowding:
\(
u_{max} = 0,072 \left(\frac{30,5}{R}\right)^{1,1} \left(\frac{3050}{c}\right)^{1,4} \left(\frac{w}{4,54}\right)^{0,7} \left(\frac{2,4}{\rho}\right)^{0,7} (mm)
\\
v_{max} = 18,3 \left(\frac{30,5}{R}\right)^{1,46} \left(\frac{w}{4,54}\right)^{0,48} \left(\frac{2,4}{\rho}\right)^{0,48} (mm/s)
\\
a_{max} = 0,81 \left(\frac{30,5}{R}\right)^{1,84} \left(\frac{c}{3050}\right)^{1,45} \left(\frac{w}{4,54}\right)^{0,28} \left(\frac{2,4}{\rho}\right)^{0,28} (g)
\)
No grafico acima, os pontos \( 1 \text{ e } 2 \) são calculados como os pares [velocidade ; frequencia] assim:
\(
p_1 = [v_{\text{max}};\frac{v_{\text{max}}}{2\pi u_{\text{max}}}]
\\
p_2 = [v_{\text{max}};\frac{a_{\text{max}}}{2\pi v_{\text{max}}}]
\\
ou
\\
p_2 = [v_{\text{max}};\frac{a_{\text{max}}}{(2\pi u_{\text{max}})^2}]
\)
Mas só podemos utilizar estas equações se assumirmos que o erro por aproximarmos a oscilação por uma senoide é pequeno, ou, dito de outra forma, que essa aproximação não interfere demais na nossa análise; lembre-se disso.
Agora você tem dois caminhos: pode utilizar os limites de frequência dados pelo deslocamento e aceleração máximos, ou, ainda, utilizar a velocidade máxima aliada a todo o espectro de frequência abaixo das linhas isometricas de deslocamento e aceleração. Lembre-se que estamos trabalhando com modelos que preveem o máximo do deslocamento, velocidade e aceleração. Assim, os valores de frequencias associados as linhas isométricas destes valores podem ser considerados como plausíveis de ocorrerem se a aproximação senoidal pode ser considerada.
Aplicando os limites da NBR 9653.
A NBR 9653 estabelece limites para a velocidades de vibração medidas no terreno, vou repetir, só para garantir: NO TERRENO. Você já viu no texto acima que não pode medir as vibrações na estrutura para aplicar a norma, senão estará medindo a resposta da estrutura a vibração, que, inclusive, pode ser muito inferior a gerada pelo desmonte.
Esses limites são especificados em função da frequência de vibração, sendo definidos por faixas que associam valores de velocidade de partícula (em mm/s) à frequência medida (em Hz).
A tabela de limites da norma é:
| Faixa de frequências (Hz) | Limite inferior (mm/s) | Limite superior (mm/s) | Taxa (mm/s) / (Hz) |
| [4 – 15) | 15 | 20 | 0,45 |
| [15 – 40] | 20 | 50 | 1,2 |
| > 40 | 50 | 50 | 0 |
A tabela acima diz que as frequencias associadas as medições de velocidade de partícula devem obedecer a três curvas distintas:
| Faixa de frequências \(f (Hz)\) | Velocidade limite \(v (mm/s)\) |
| [4 – 15) | \(v = 0,45f + 13,18\) |
| [15 – 40] | \(v=1,2f + 2 \) |
| > 40 | \(v=50\) |
Se você está se perguntando quais componentes, longitudinal, transversal ou vertical, devem obedecer esta tabela? A resposta é: todas. Tanto faz, você não pode gerar velocidades acima das curvas da tabela para qualquer componente.
Mas como se associa um valor de frequencia a um valor de velocidade de partícula no sismograma? Existem alguma técnicas para isso. A mais computacionalmete barata e mais usada é o método de meio período por zero crossing.
Este método consiste em analisar os pontos onde o sinal de velocidade cruza o zero, ou seja, onde muda de positivo para negativo (ou vice-versa). Se o sinal for aproximadamente senoidal, os cruzamentos com zero ocorrem a cada meio período da oscilação. Assim, ao medir o tempo entre dois cruzamentos consecutivos, podemos estimar a frequência local como:
\(f = \frac{1}{2 \cdot \Delta t}\)
Onde \(\Delta t\) é o tempo entre dois cruzamentos consecutivos com a linha zero.
A esmagadora maioria dos fabricantes de sismógrafo usam esta técnica para calcular as frequências associadas a cada valor de velocidade medido. Existem outras maneiras de se estimar a frequencia, mas esta é, sem dúvida, a mais usada. Ela produz uma tabela com valores de velocidade de partícula x frequencia. Ou seja, cada valor de velocidade de partícula medido tem associado uma frequência de oscilação. Diga-se de passagem, nos bons sismografos, você pode exportar este dados em forma de uma tabela.
Com base nesta tabela de velocidade x frequencia você pode saber se seu desmonte atende a NBR 9653. Basta aplicar as equações da tabela acima de acordo com a frequencia medida.
Muitas, mas muitas, pessoas usam apenas as frequencias associadas aos valores de pico e aplicam os limites da NBR 9653. Mas, se você entendeu, pelo menos a explicação da resposta da estrutura, já sabe por que não pode usar apenas os valores de pico. Veja este outro texto que explica, talvez, de uma maneira um pouco mais simples do porque não usar valores de pico apenas.
E se você está simulando as frequências de um desmonte, poderá, como eu disse acima, optar por dois caminhos guiados pelo gráfico tripartido:
- 1 – pode utilizar os limites de frequência dados pelo deslocamento, velocidade e aceleração máximos para obter a a faixa provável das frequências principais, isto é, áquelas associadas aos valores máximos;
- 2 – pode utilizar as velocidades máxima e mínima aliadas a todo o espectro de frequência abaixo das linhas isometricas de deslocamento e aceleração maximos.
Seguir pelo caminho 1 é bem simples, basta obter a velocidade máxima do modelo é calcular qual é a frequencia associada a aceleração e ao deslocamento máximos, assim:
\(
v_{ \text{max} } = u 2 \pi \omega_{nv} \Rightarrow \omega_{nv} = \frac{ v_{ \text{max} } }{2u(x)\pi}
\\
a_{ \text{max} } = (u 2 \pi)^2 \omega_{na} \Rightarrow \omega_{na} = \frac{ a_{ \text{max} } }{(2u\pi)^2}
\)
O valor de \(\omega_{nv}\) vai te dar o valor mínimo da provável frequencia; Já o valor de \(\omega_{na}\), o valor máximo
O caminho 2 requer uma modelagem um pouco mais refinada. Deve-se estimar os extremos da velocidade de partícula, isto é, os valores máximos e mínimos prováveis. Assim, “caminhamos” por curvas isometricas de deslocamento e aceleração que conectam os extremos de velocidade de partícula.
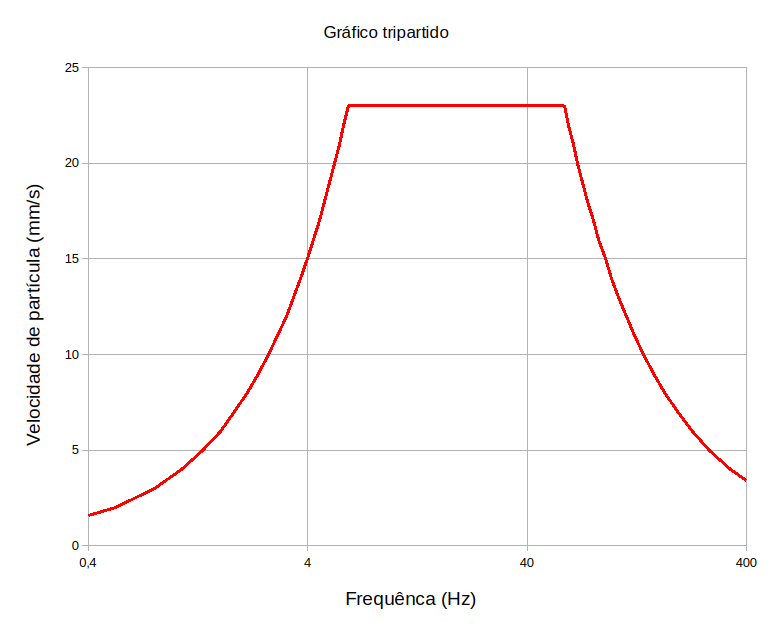
Por exemplo, digamos que nosso modelo tenha retornado os seguintes valores:
\(
u_{\text{max}} = 0,6\,mm\\
v_{\text{max}} = 23\,mm/s\\
a_{\text{max}} = 8526\,mm/s^2
\)
Com o uso das relações:
\(
u = \text{constante}\\
v = 2\pi f \cdot u\\
a = \text{constante}\\
v = \frac{a}{2\pi f}
\)
Obtemos o gráfico tripartido abaixo:
As frequências principais, ou seja, associadas aos maiores valores de velocidade de partícula, são aquelas presentas na área destacada na figura abaixo:
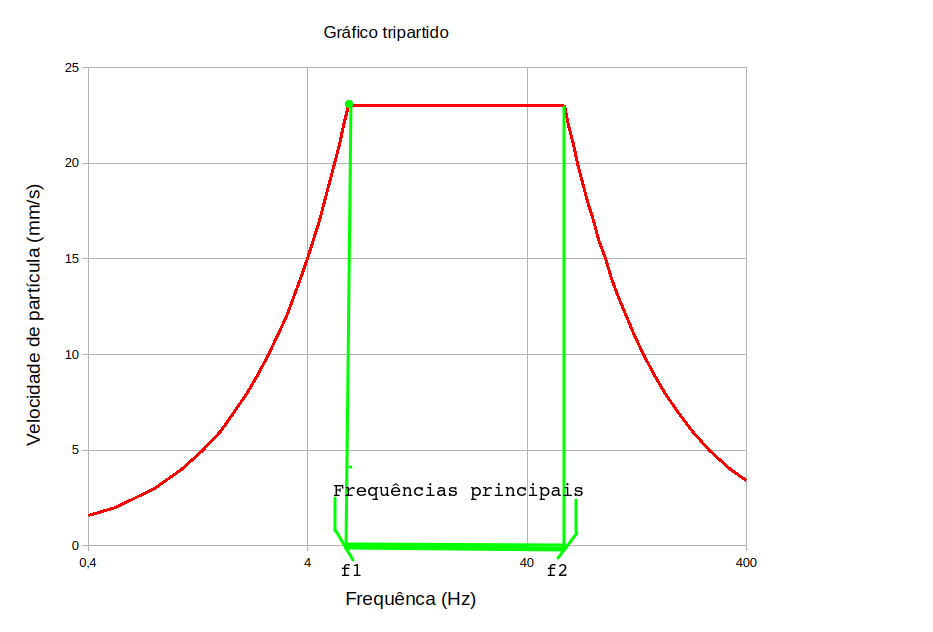
Este intervalo de frequencias principais é facilmente encontrado, desta forma:
\(
f_1 = \frac{v_{max}}{2\pi u_{max}} = \frac{23}{2\pi \cdot 0,6} \approx 6,1\,Hz
\\
f_2 = \frac{a_{max}}{2\pi v_{max}} = \frac{8526}{2\pi \cdot23} \approx 59\,Hz
\)
Você pode usar estes valores se quiser simular as frequências principais, isto é, àquelas associadas aos valores máximos de velocidade de partícula que seu modelo prevê. Mas lembre-se, ao fazer isso você ignora o restante do espectro. Veja na figura abaixo onde todas as possíveis frequências do desmonte são destacadas com o uso de um modelo que prevê tanto o valor máximo quanto o mínimo de velocidade de partícula.
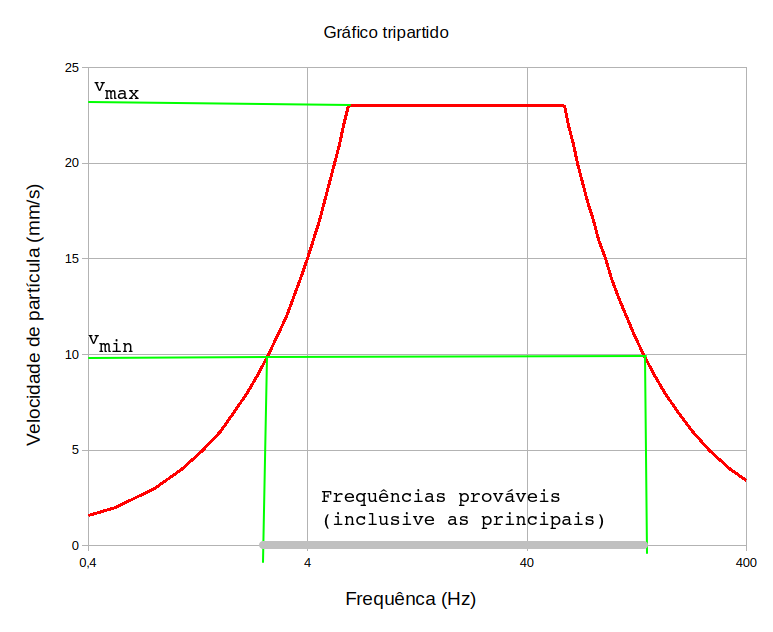
Veja a tabela abaixo onde estão incluídas algumas frequências simuladas utilizando \(v_{min}\) e \(v_{max}\):
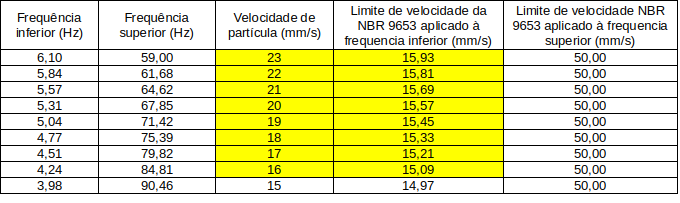
A parte destacada em amrelo são os valores simulados que não atendem a norma. Veja na figura abaixo onde destacamos os valores que não atendem a NBR 9653.
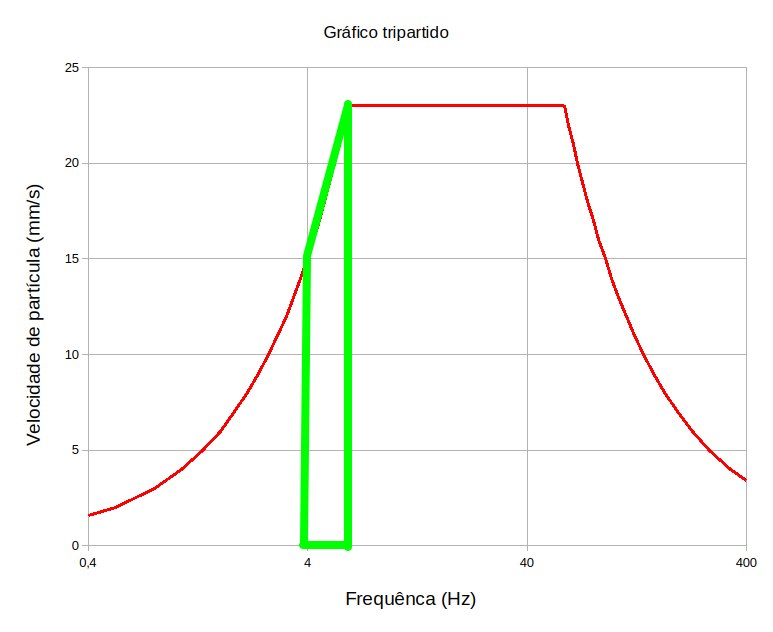
Incluíndo o o sequênciamento na simulação de frequências.
Vamos reforçar uma hipótese: se você está suficientemente próximo ao desmonte e o meio tem uma homogeniedade adequada, então você pode aproximar as vibrações por uma senoide sem grandes prejuízos à verdade. Se estas condições são aceitas, devemos verificar se as frequências induzidas pela temporização das cargas explosivas está contida no intervalo das frequências principais. Caso não estejam, devemos aumentar o intervalo para incorporar essas frequências.
Vamos começar com um modelo bem simples: dois furos separados por um retardo de 25ms.
Sem considerar qualquer tipo de dispersão, temos um período \(T= 25ms = 0,025s\), logo temos um frequência de:
\(
f = \frac{1}{T} = \frac{1}{0,025} = 40 Hz
\)
Agora, observe o sequenciamento representado na imagem abaixo:
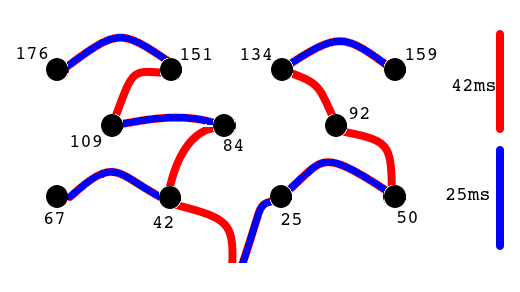
Neste desmonte foram utilizados tempos de 25ms e 42ms, se você tentar calcular as possíveis frequências como:
\(
f_1 = \frac{1000}{25} = 40 Hz
\\
f_2 = \frac{1000}{42} \approx 24 Hz\)
estará cometendo um erro. Não interessa os tempos nominais dos retardos, mas a diferença de tempo entre as sequencias de detonação. Veja a tabela abaixo onde calculamos as frequências deste desmonte através da dieferença entre as sequências.
| Sequência (ms) | Períodos (ms) | Frequências (Hz) |
| 25 | 17 | 58,82 |
| 42 | 8 | 125,00 |
| 50 | 17 | 58,82 |
| 67 | 17 | 58,82 |
| 84 | 8 | 125,00 |
| 92 | 17 | 58,82 |
| 109 | 25 | 40,00 |
| 134 | 17 | 58,82 |
| 151 | 8 | 125,00 |
| 159 | 17 | 58,82 |
| 176 |
Utilizando os mesmos valores de \(u_{\text{max}} = 0,6\,mm \,,\, v_{\text{max}} = 23\,mm/s \, ,\,a_{\text{max}} = 8526\,mm/s^2\) vemos que a frequência de 125 Hz presente na tabela fica fora da previsão das frequências principais, neste caso, precisamos incluí-la. O gráfico tripartido abaixo mostra como se dá essa inclusão.
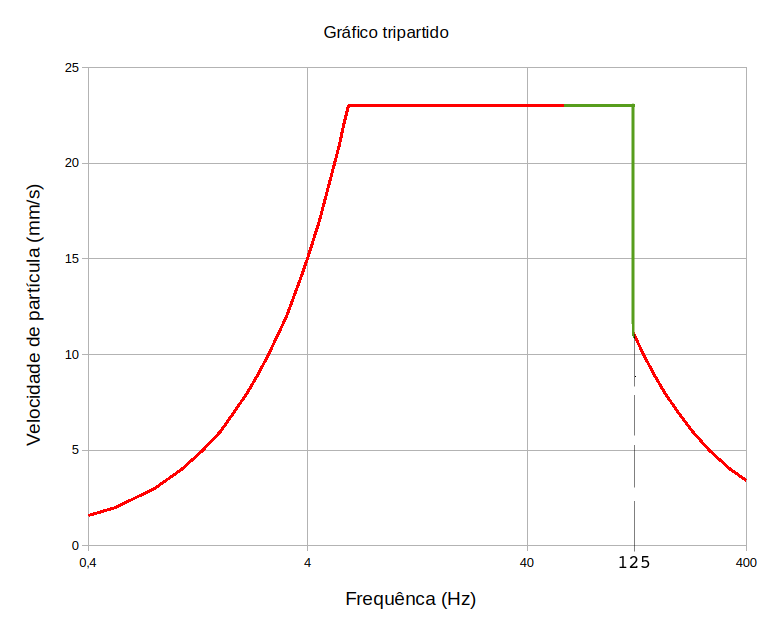
Mas você deve ter cuidado. O calculo de frequências, principalmente quando se usa não-elétricos, pode conduzir a previsões errôneas se você não considerar a dispersão dos detonadores.
Em desmontes de subsolo, por exemplo, é muito comum a realização do sequenciamento com o escalonamento de tempos dos não-elétricos, ou seja, faz-se a sequência no fundo do furo, utilizando diversos tempos para tal.
A tabela abaixo é o resultado de uma simulação considerando alguns valores de dispersão para diversos tempos de não-elétricos. Ela mostra a probabilidade de se obter frequencias menores que 20 Hz somente pela constatação de que os não-elétricos possuem dispersão e não iniciam exatamente ao mesmo tempo, ou seja, possuem um retardo natural entre si.
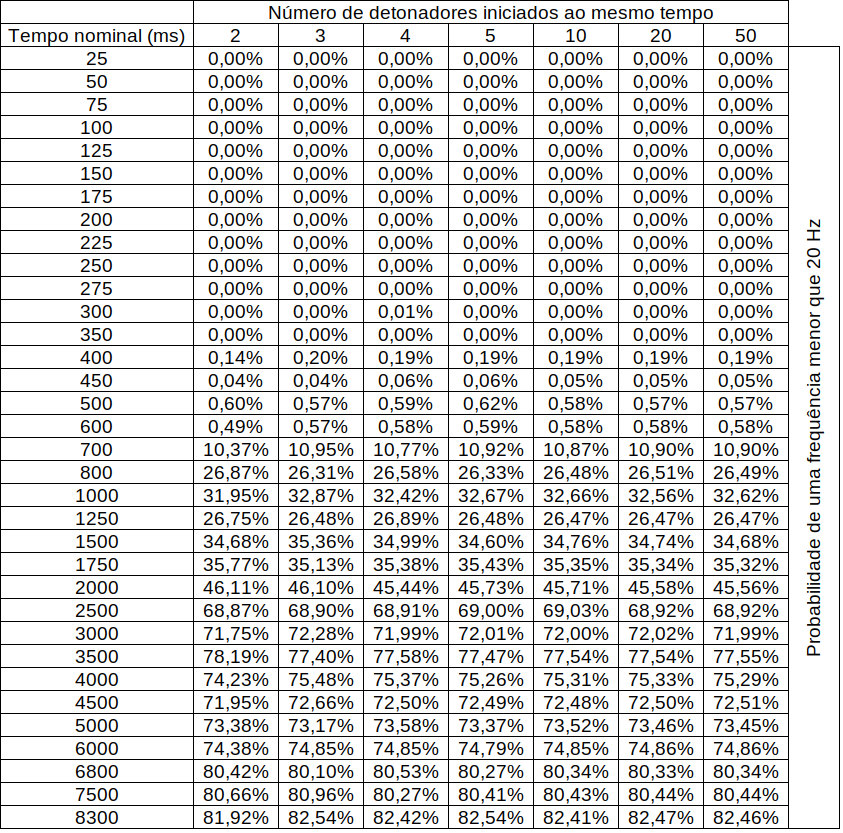
Veja que tempos mais altos tendem a serem os mais problemáticos.
Este é só um exemplo para te mostrar que o estudo de frequências é muito amplo, diversos fatores devem ser levados em consideração.
Um pequeno epílogo.
Eu já presenciei situações de interpretações completamente errôneas da NBR 9653. Já ouvi muitos limites de velocidade de partícula que foram “inventados” e associados, de maneira equivocada, a NBR 9653. Existe um fetiche, por exemplo, com o valor de 15mm/s. De fato, na antiga NBR 9653 de 1986 este era o limite, independente de frequências. Também já vi 18mm/s, 20mm/s e até maiores, 50mm/s, serem apresentados como valores seguros e vinculados como sendo extraídos na NBR 9653. Nada mais equivocado. Não porque, de certa forma, estes valores não sejam seguros, mas por que não existem estes valores como limites na NBR 9653. Existem diversos limites de acordo com a frequência associada, simples. Nada impede de serem usados, o que não se deve fazer é tentar vincular estes valores, que são mais oriundos de palpites do que da ciência do desmonte de rochas, a NBR para tentar dar um verniz de tecnicidade.
Outras situações são quando estes limites baseados apenas em velocidade de partícula são muito baixos onde não há necessidade para tal. Em uma obra de escavação subterrânea em uma capital brasileira a muitos anos atrás eu presenciei a imposição de um limite de 15mm/s como um valor seguro a ser seguido. Tudo bem, de fato é seguro, mas as consequências, de prazo e financeiras, ao se impor tal restrição não foram levadas em conta. Existe uma norma que te permite alcançar valores muito maiores, basta saber projetar seu desmonte e segui-la. Nesta obra, eu presenciei a instalação de sismógrafos nos andares mais altos dos prédios, sobre calçadas, enfim em todos os lugares possíveis onde não se deve instalar para captar os valores a serem comparados com a NBR 9653. Esta metodologia fez o óbvio: mascarou as vibrações medindo as respostas das estruturas. Uma bela engenharia. Também em mais de 3000 captações simográficas não foi feito nem um esboço, nem uma tentativa de se deduzir um modelo de previsão por que se acreditava que, como os valores das sismografias estavam atendendo o fetiche dos 15mm/s, não era necessário. Mas o que acontecia na verdade é que todos estavam medindo respostas de estruturas, mas a vibração real que chegavam a elas passava, as vezes, de 150mm/s (sim, eu fiz algumas medições, digamos, corretas, para nosso uso interno).
Estas abordagens baseadas em palpites, principalmente o palpite famoso dos 15mm/s, lembra muito as técnicas usadas nas pseudociências, como a frenologia, descrita no inicio deste texto. Geralmente estes limites inventados vem acompanhado de um apelo à autoridade, falácia clássica das pseudociências e de referências obscuras, como trabahos e livros de conteúdos bem duvidosos.
E a suposta “falta de danos” quando se adota estes limites demasiados restritivos é, quase sempre, coroada com a argumentação falaciosa conhecida como post hoc ergo propter hoc. O discurso é mais ou menos esse: “Se adotamos 15mm/s de limite e não ocorreram danos, então o limite esta certo”. Isso é um argumento bem infantil. Veja só, eu vou escrever uma combinação de letras e simbolos abaixo:
QLKFJ&*¨$#vbnppppp******
Estes simbolos, caro leitor, segundo a mística tradição dos polinésios do seculo II lhe protege de tigres. Duvida? Olhe ao seu redor agora e veja se existe um tigre te atacando. Percebeu a conexão com os supostos danos evitados pelos 15mm/s?
Precisamos cuidar um pouco mais da engenharia de explosivos para não transforma-la em um reino de palpites, cheia de chavões e referências circulares a idéias e conceitos equivocados. E isso vale para outras áreas também; as vezes ouço coisas que sinceramente não sei de onde vieram ou como foram deduzidas. Já ouvi que cordel detonante funciona como um micro-booster. Sério? Acho que falta muito conhecimento para uma pessoa falar isso, falta o conhecimento de run up, run down e da teoria básica da iniciação da massa explosiva. E tem muitas outras, como o famoso “gas” que existe dentro dos tubos de choque, outra lenda que não sei de onde veio.
O perigo mora quando estas ideias são usadas para o projeto do desmonte. Podemos estar criando situações de alto risco, assim como o famoso detector de bombas ADE 651, que cotinha a mesma tecnologia daquelas varinhas que o pessoal usa para, supostamente, encontrar água subterrânea: acabou matando muitas pessoas.

Excelente artigo! Parabéns
Super texto, Golin! Congrats