Look out e volume na escavação de túneis e galerias.

Uma das coisas que diferencia uma cavidade natural, como uma caverna, por exemplo, de outra aberta intencionalmente é que esta última possui em sua concepção um gabarito idealizado. Uma seção de um túnel tenta ser a mais próxima de uma seção idealizada, projetada por alguem. Mas seções transversais reais escavadas dificilmente são cópias fiéis das suas primas idealizadas na prancheta. Existem inúmeros ruídos na escavação que deformam a idéia ideal. Geologias complexas, erros de perfuração, carga explosiva e outras variáveis introduzem alguma entropia na forma. As limitações da tecnologia inerentes à abertura de túneis com explosivos dificilmente podem ser ignoradas neste contexto. O projeto de um contorno idealizado sobre um circunferência, elipse ou qualquer outra seção cônica não pode ser executado com perfeição. No limite, para se obter um contorno preciso, os furos deveriam ter distâncias entre si tendendo a zero. Isso é inexequível.

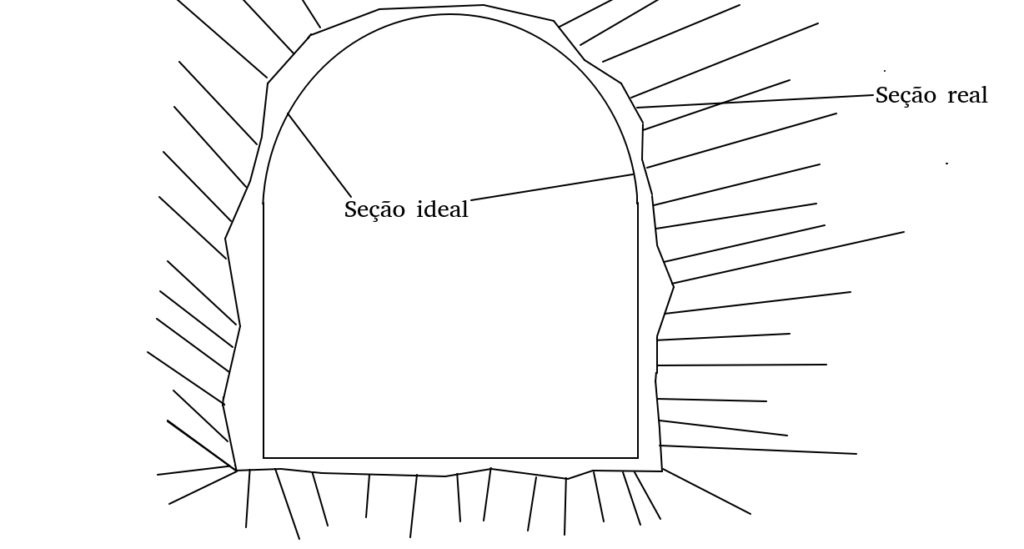
Um das condições de afastamento da idealidade sem a qual não é possível escavar um túnel com explosivos é o look out. Eu não conheço uma tradução adequada ao português desta palavra. Muito confundem o “overbreak” ou sobrequebra com look out. São conceitos diferentes. A ocorrência de overbreak não é, em essência, algo intencional; o look out precisa ser intencional. Sem o look out não conseguimos recuperar a seção idealizada no decorrer dos avanços. Isso ocorre porque a perfuratriz precisa de um espaço mínimo para a sua operação.

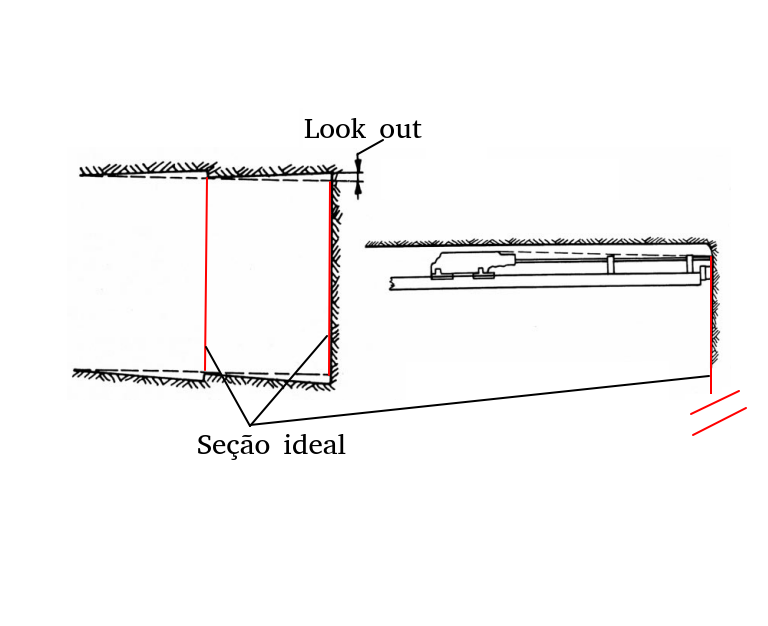
Perceba que tanto o look out quanto o overbreak só tem uma existência definida se comparados com uma seção previamente idealizada. Não existe sentido em se calcular o overbreak de uma caverna.
Existem dois objetivos neste texto:
1 – Tentar entender como o look out influencia no volume idealizado da escavação e na forma da seção ideal.
2 – Como podemos inferir à seção real escavada parâmetros estatisticos que nos dizem o quão próxima ela esta da seção ideal.

Você pode projetar o look out de inúmeras maneiras. Pode inclusive determinar valores distintos para cada parte do perímetro ou mesmo para grupos distintos de furos.

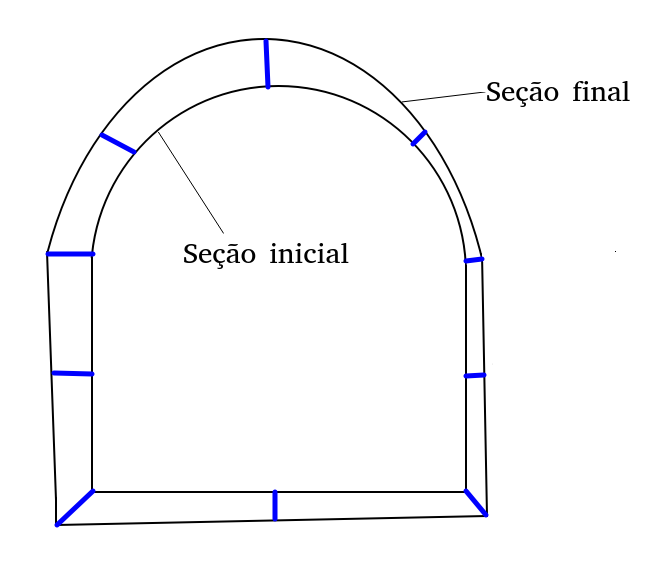
Mas para facilitar o nosso desenvolvimento, vamos considerar que a seção final é uma transformação homotética. Isso preserva de certa forma as proporções da seção ideal projetada.

Podemos imaginar isso como a sobra projetada por uma fonte de luz.

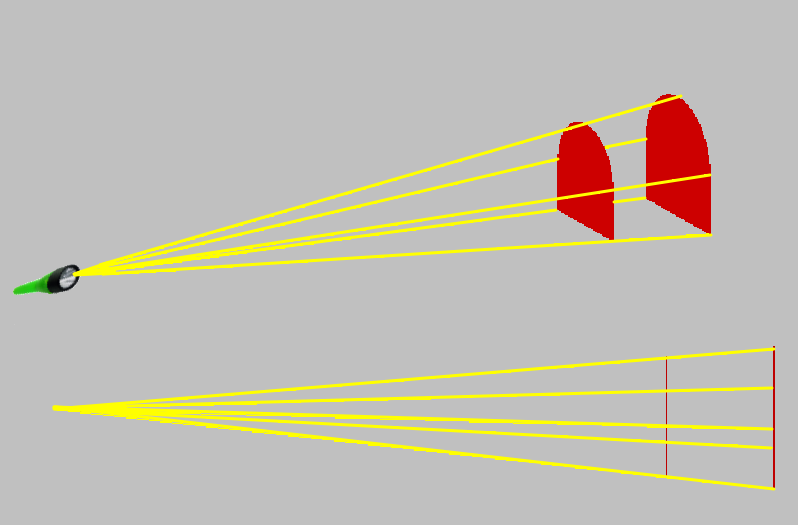
O volume que nos interessa é o volume da “sombra”, representado em vermelho na figura abaixo.

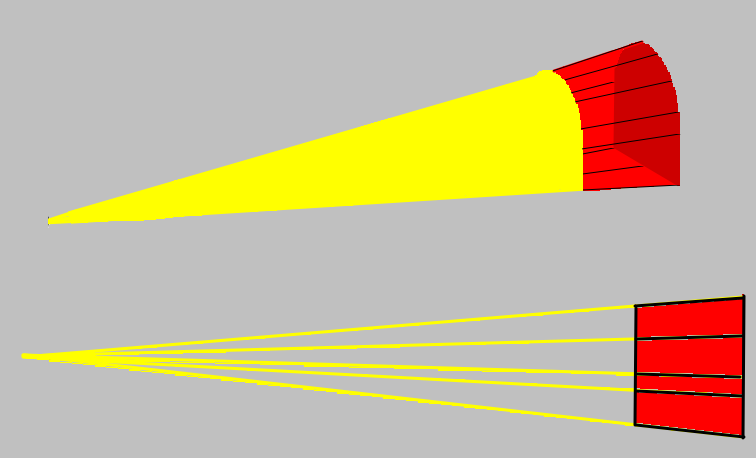
Este volume (V) é calculado como a diferença entre o volume 2 e o volume 1, conforme mostrado na figura abaixo.

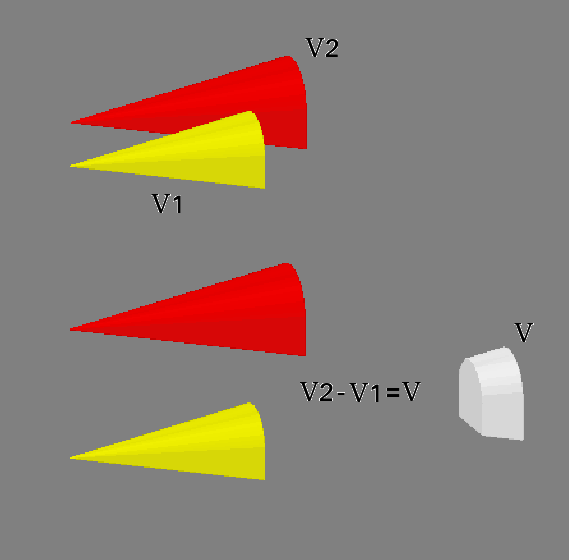
Existem diversas abordagens possóveis para se calcular V. Como estamos tratando de uma projeção homotética da seção, podemos considerar as linhas imaginárias que partem do ponto de origem como um campo vetorial e utilizar o teorema do divergente para encontrar o volume.

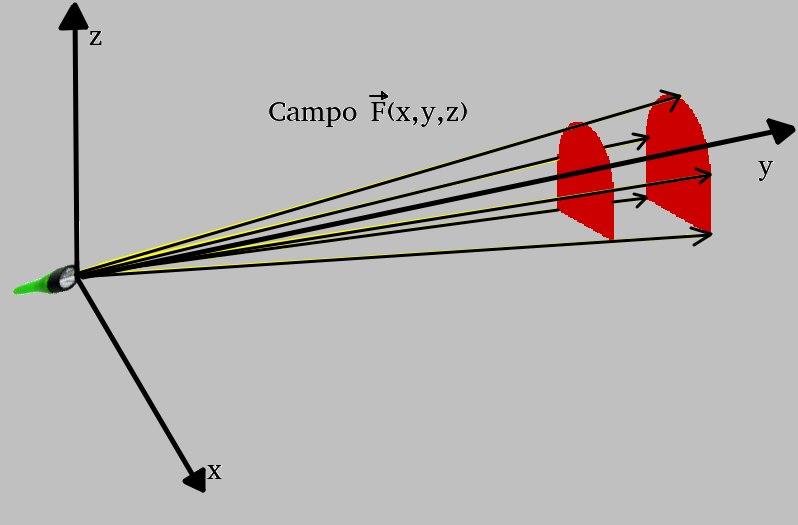
As normais da superfície do volume, a menos das seções transversais, são perpendiculares ao campo. Veja na figura abaixo.

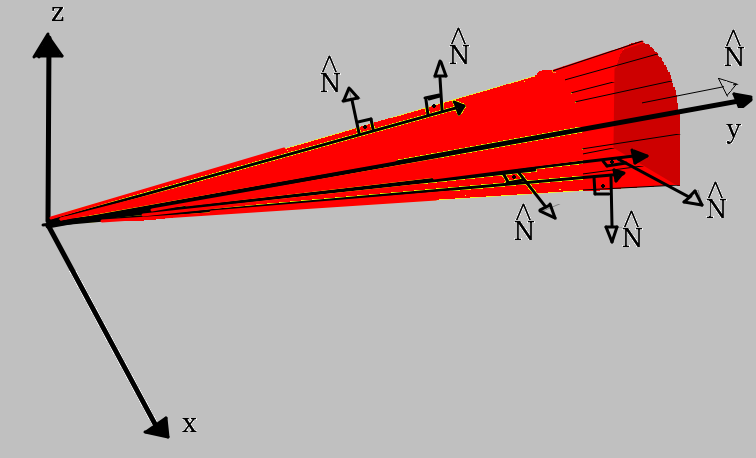
O teorema do divergente, também conhecido com teorema de Gauss, é:

\( \iiint_V\nabla \cdot \vec{F} dV= \iint_S \vec{F} \cdot \hat{N} dS\)

A equação acima diz que o divergente do campo \( \vec{F} \) sobre um volume \(V\) é igual ao fluxo do campo sobre a superfície \((S)\) que delimita \(V\).
Você não precisa se preocupar com o significado físico do nosso campo \( \vec{F} \). Aqui ele é apenas um artifício matemático, escolhido de forma providencial, para nos ajudar a calcular o volume \(V\). E, conforme já deve ter notado, é dado por:

\( \vec{F} = (x,y,z) \)

Significa que para cada ponto \( (x,y,z) \) associamos um vetor cujos valores das componentes são as próprias componentes.
Uma visão deste campo em 2D, que fiz aqui, é mostrada na figura abaixo.

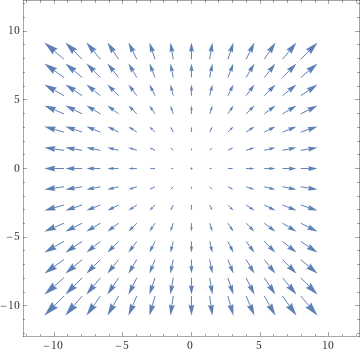
Vamos começar pela integral da esquerda. A definição de divergente é esta:

\( div \vec{F} = \nabla \cdot \vec{F} = [\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z} ] \cdot [F_x,F_y,F_z]^{T} \)

No nosso caso, teremos

\( \nabla \cdot \vec{F} = [\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z} ] \cdot [x,y,z]^{T}
\\
= \frac{\partial}{\partial x} x + \frac{\partial}{\partial y} y+\frac{\partial}{\partial z} z = 1+1+1 = 3
\)

Substituindo temos:

\(
\iiint_V\nabla \cdot \vec{F} dV= \iint_S \vec{F} \cdot \hat{N} dS
\\
\iiint_V 3 dV = \iint_S \vec{F} \cdot \hat{N} dS
\\
3 \iiint_V dV = \iint_S \vec{F} \cdot \hat{N} dS
\\
3V = \iint_S \vec{F} \cdot \hat{N} dS
\)

No desenvolvimento acima, perceba que a integral

\(
\iiint_V dV
\)

é simplesmente o volume do sólido.
A integral de fluxo pode ser dividida em duas, cada uma responsável por uma superfície do nosso volume. As superfícies são as mostradas na figura abaixo.

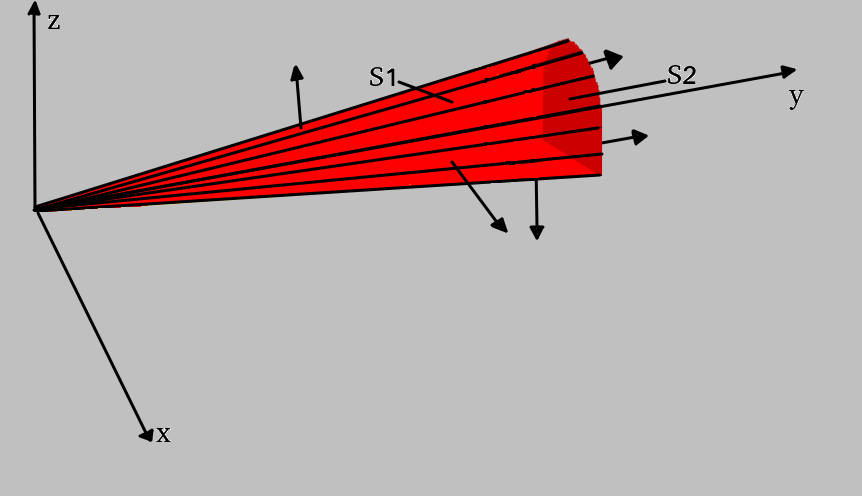
Deste modo, podemos reescrever a integral de fluxo:

\(
\iint_S \vec{F} \cdot \hat{N} dS = \iint_{S_1} \vec{F} \cdot \hat{N_1} dS_1 + \iint_{S_2} \vec{F} \cdot \hat{N_2} dS_2
\)

Veja, todas as normais da superfície \(S_1\) são perpendiculares ao campo. Isso anula o produto interno

\(
\vec{F} \cdot \hat{N_1} = 0
\)

A normal da superfície \(S_2\) contem apenas a componente em \( y \). E o produto interno do campo com a normal de \(S_2\) fica:

\(
\vec{F} \cdot \hat{N_2} = [x,y,z]\cdot [0,1,0]^T = y
\)

Veja que considerar a normal de \( S_2 \) como sendo o vetor \( [0,1,0] \) implica que a projeção do campo deve ser paralela à superfície \( S2 \). Falando de outro modo, o desenvolvimento até aqui considera que a lanterna não pode ser inclinada em realação a \( S2 \). Além disso, a escolha do ponto de origem da homotetia determina como será a ampliação da seção.

A integral de fluxo então torna-se

\(
\iint_S \vec{F} \cdot \hat{N} dS = \iint_{S_1} \vec{F} \cdot \hat{N_1} dS_1 + \iint_{S_2} \vec{F} \cdot \hat{N_2} dS_2
\\
= 0 + \iint_{S_2} y dS_2
\)

Agora, observe que o elemento de área \( dS_2 \) não possui componente no eixo \(y\), \( dS_2 = dxdz \) e y torna-se uma constante.

\(
\iint_{S_2} y dS_2 = \iint_{S_2} y dxdz = y \iint_{S_2} dxdz
\\
= yA_2
\)

Veja que o termo

\(
\iint_{S_2} dxdz
\)

é somente a área da seção \(A_2\). Entenda \(y\) aqui como a distância do ponto de origem da homotetia até a seção \(S_2\). Juntando tudo

\(
3V = \iint_S \vec{F} \cdot \hat{N} dS
\\
3V = yA_2
\\
V = \frac{1}{3}yA_2
\)

Para o nosso volume V temos que

\(
V = V_2 – V_1
\\
V = \frac{1}{3}y_2A_2 – \frac{1}{3}y_1A_1
\\
V = \frac{1}{3}(y_2A_2 – y_1A_1)
\)

Na equação acima, \(A_2\) é a seção final e \(A_1\) a seção original. Da mesma forma, \(y_1\) e \(y_2\) são as distâncias do ponto de origem até as seções \(A_1\) e \(A_2\) respectivamente.

A partir deste ponto o desenvolvimento deve ser particularizado de acordo com a forma da seção transversal.
Vamos utilizar uma seção muito comum para tuneis e galerias, veja a figura abaixo.

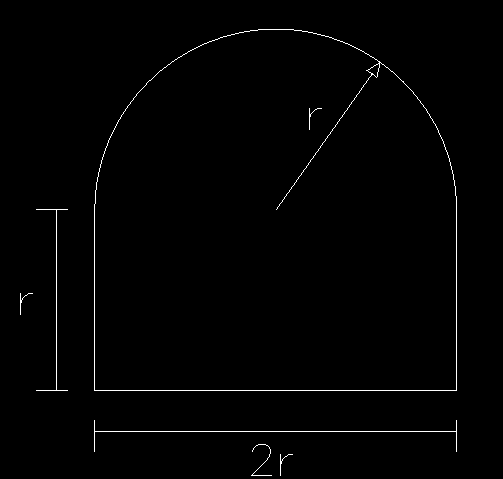
Como estamos lidando com uma ampliação por homotetia, a seção final, ou seja, com a adoção do look out é esta da imagem abaixo

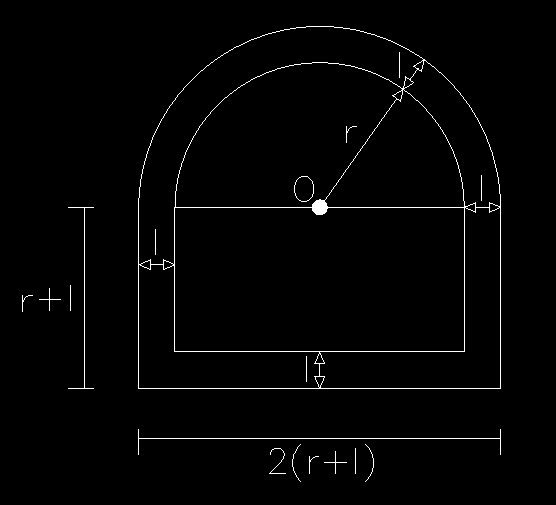
Repare que esta seção aliada a escolha do ponto O faz com que o look out seja igual para todos os trechos do perímetro. Se tivessemos uma seção diferente, por exemplo a da imagem abaixo, a situação não seria a mesma.

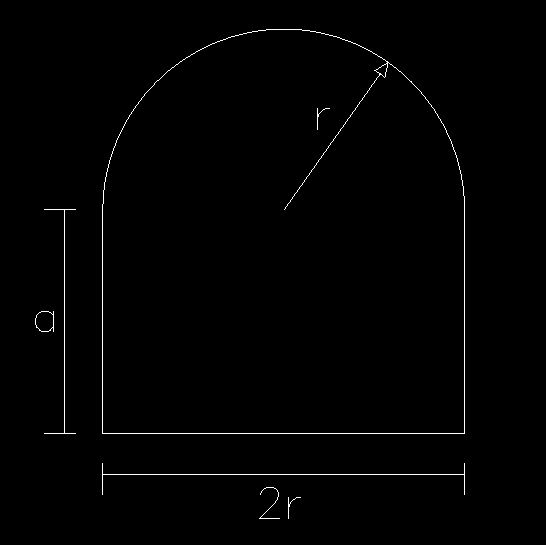
Nesta situação \( a \neq r \) e o look out da sapateira (piso) será diferente do look out da aboboda.

Agora, façamos um corte transversal no volume maior.

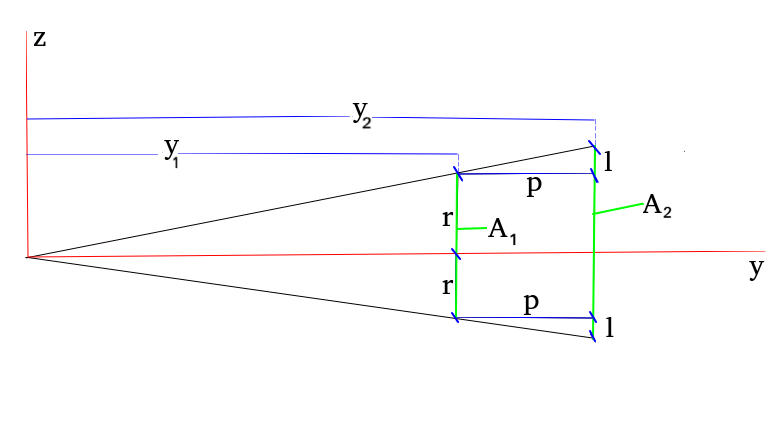
A seção \( A_2 \) é uma ampliação de \( A_1 \). Pela figura, a razão da homotetia \( (k) \) é

\(
k = \frac{r+l}{r}
\)

E a razão entre as áreas é:

\(
\frac{A_2}{A_1} = k^2 = \frac{(r+l)^2}{r^2}
\)

A variável \(l\) é o comprimento do look out.
Podemos reescrever a equação do volume em função da área original \(A_1\):

\(
\frac{A_2}{A_1} = \frac{(r+l)^2}{r^2}
\\
A_2 = A_1 \frac{(r+l)^2}{r^2}
\\
\\
V = \frac{1}{3}(y_2A_2 – y_1A_1)
\\
V = \frac{1}{3}(y_2A_1 \frac{(r+l)^2}{r^2} – y_1A_1)
\\
V = \frac{A_1}{3}(y_2 \frac{(r+l)^2}{r^2} – y_1)
\)

Agora, colocaremos as distâncias \(y_1\) e \(y_2\) em função do avanço \(p\). Observe que por semelhança de triângulos temos que:

\(
\frac{r}{y_1}=\frac{l}{p}
\\
y_1=\frac{rp}{l}
\)

E também

\(
\frac{(r+l)}{y_2}=\frac{l}{p}
\\
y_2=\frac{p(r+l)}{l}
\)

Substituindo na equação do volume:

\(
V = \frac{A_1}{3}(y_2 \frac{(r+l)^2}{r^2} – y_1)
\\
V = \frac{A_1}{3}(\frac{p(r+l)}{l} \frac{(r+l)^2}{r^2} -\frac{rp}{l})
\\
V = \frac{A_1}{3}(\frac{p(r+l)^3}{lr^2} -\frac{rp}{l})
\\
V = \frac{A_1p}{3lr^2}((r+l)^3 – r^3))
\)

Se você expandir, por exemplo, o polinomio \( (r+l)^3 – r^3 \) vais encontrar:

\(
V = A_1p\left(1+\frac{l}{r}+\frac{1}{3}\left(\frac{l}{r}\right)^2\right)
\)

Você pode também abrir a área \(A_1\) para obter um equação explicitamente dependente de \( (l,r,p) \). Mas o que quero te mostrar aqui é a variação do volume em função do look out, \(l\). No nosso caso, a área \(A_1\) não depende do look out, então:

\(
\frac{\partial V}{\partial l}=A_1p\left(\frac{1}{r}+\frac{2l}{3r^2}\right)
\)

Agora calculamos o volume somente do look out:

\(
V_l = V – A_1p
\\
V_l = A_1p\left(1+\frac{l}{r}+\frac{1}{3}\left(\frac{l}{r}\right)^2\right) – A_1p
\\
V_l = A_1p\left(\frac{l}{r}+\frac{1}{3}\left(\frac{l}{r}\right)^2\right)
\)

Podemos ver que a taxa de variação do volume da seção em função do look out é unica:

\(
\frac{\partial V_l}{\partial l}=A_1p\left(\frac{1}{r}+\frac{2l}{3r^2}\right) = \frac{\partial V}{\partial l}
\)

Veja que a taxa de aumento do volume em função do look out corresponde a multiplicação da extrusão da área original \( A_1 \) através do avanço \( p \) pelo termo \( \frac{1}{r}+\frac{2l}{3r^2} \).

A proporcionalidade inversa do raio \( r \) diz que seções “menores” tendem a sentir mais o efeito do look out.
Seções pequenas onde a preocupação com a diluição do minério é grande serão muito sensíveis ao aumento do look out.

Isso pode ser um dos pilares da justificativa de navegação da perfuração em equipamentos menores.

Outa informação que podemos verificar é que a taxa de aumento do volume em função do avanço \(p\) não depende do próprio avanço. Veja

\(
V = \frac{A_1p}{3lr^2}((r+l)^3 – r^3))
\\
\frac{\partial V}{\partial p}=\frac{A_1}{3lr^2}((r+l)^3 – r^3))
\)

Isso significa que, no nosso caso, tanto faz para o calculo de volume total se usamos um look out \(l\) para cada desmonte de avanço \(p\) ou se usamos o mesmo look ou \( l \) para o comprimento total do túnel. Veja, se o comprimento total do túnel é \(T\) então

\(
T = \sum_{k=1}^n p_k
\\
\frac{A_1}{3lr^2}((r+l)^3 – r^3)) T = \frac{A_1}{3lr^2}((r+l)^3 – r^3)) \sum_{k=1}^n p_k = V_T
\)

Na equação acima \( n \) corresponde ao total de avanços e \( p_k \) é o k-ésimo avanço.

Outro fator interessante é observar quantos avanços correspondem a um volume de look out igual a um volume ideal.
O volume idealizado de look out é a diferença entre o volume com look out e a extrusão pura da área original \( A_1 \):

\(
V_l = V – A_1p
\\
V_l = \frac{A_1p}{3lr^2}((r+l)^3 – r^3)) – A_1p
\\
V_l = A_1p\left( \frac{1}{3lr^2}((r+l)^3 – r^3)) – 1\right)
\)

Queremos saber quatos \( n \) fogos são necessários para escavarmos um volume ideal \( A_1p \), isto é:

\(
nV_l = A_1p
\\
n A_1p\left( \frac{1}{3lr^2}((r+l)^3 – r^3)) – 1\right)= A_1p
\\
n \left( \frac{1}{3lr^2}((r+l)^3 – r^3)) – 1\right)= 1
\\
n = \frac{1}{\left( \frac{1}{3lr^2}((r+l)^3 – r^3)) – 1\right)}
\\
n = \frac{3lr^2}{(r+l)^3 – r^3 -3lr^2}
\)

Expandindo o denominador, o que resta é:

\(
n = \frac{3r^2}{l^2+3rl}
\)

A equação acima diz quantos fogos vamos detonar até que o volume devido ao look out seja igual ao volume ideal. Essa equação vale para a nossa seção de exemplo, lembre-se disso.
Veja que o número de fogos não depende do avanço dado, mas apenas do raio da seção e do look out.
Mais uma vez observa-se que seções pequenas tedem a ter \(n\) pequenos, isto é, em poucos fogos você já escavou um volume ideal a mais.

Até aqui tratamos com seções e volumes ideais, que fazem parte de um projeto. Dificilmente a seção ideal é escavada na prática. O que podemos fazer é tentar encontrar parâmetros que nos digam o quão próximos estamos da seção ideal de projeto.

Podemos dividir a seção ideal em 6 setores, cada um responsável por uma parte do perímetro. Veja a figura abaixo

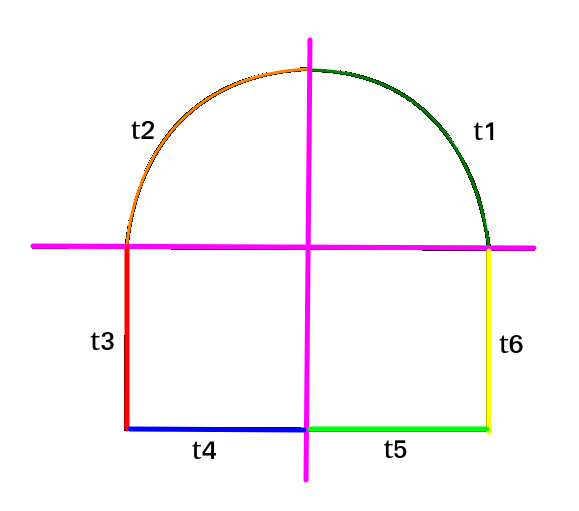
Os trechos \(t_1\) e \(t_2\) representam a aboboda. E para cada trecho, de \(t_1\) a \(t_6\) temos dois indicadores:

• Indicador de overbreak.
• Indicador de forma.

Veja por exemplo a figura abaixo.

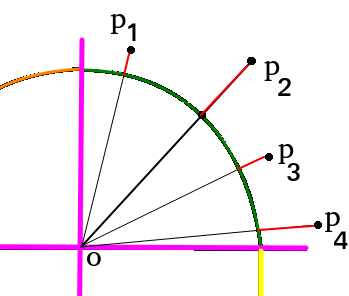
A cada ponto de \(p_1\) a \(p_4\) podemos associar um valor que mede a distância de onde está o ponto até onde deveria estar. De certa forma estamos calculando o resíduo de cada ponto, ou em termos estatisticos, o erro que cometemos quando comparamos o ponto medido com o ponto ideal. Para um conjunto de pontos qualquer pertencentes a um trecho da seção podemos utilizar a média, mediana ou mesmo o histograma dos resíduos para quantificar o over (leia-se erro cometido).

Para o indice de forma precisamos encontrar um parâmetro que nos traga a informação de quanto os pontos medidos traduzem a ideia por tras da seção idealizada. Veja a figura abaixo.

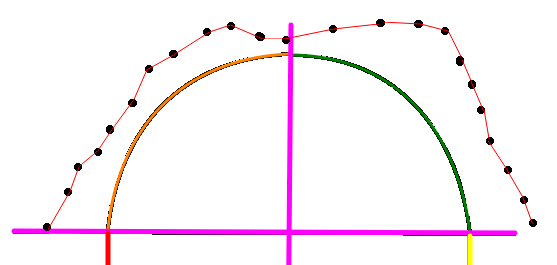
A pergunta é o quanto a seção formada pelos pontos medidos é semelhante a seção ideal?

Podemos aplicar um teste de aderência, por exemplo, para verificar se os pontos de determinado trecho de perímetro estão próximos ou não do nosso modelo.

Um teste simples que pode ser aplicado é o famoso teste de qui quadrado \(\chi^2\).

Se estamos utilizando uma planilha eletrônica, podemos retornar o valor de \(\chi^2\) facilmente.

Um exemplo de como usar as estatisticas acima. Veja a tabela abaixo.

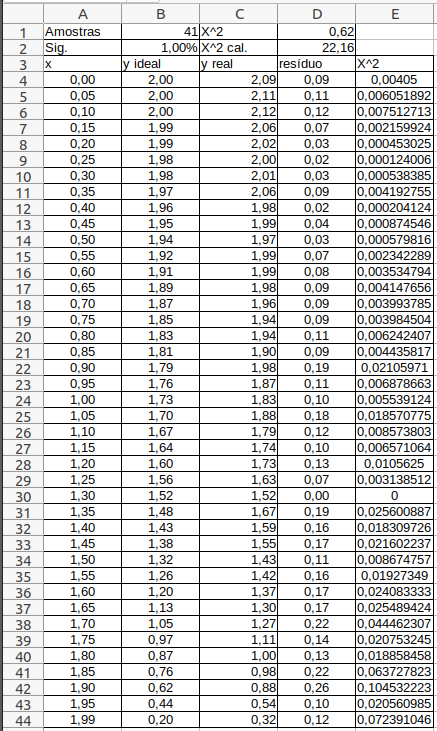
Os valores representam parte das seções ideal e da seção medida da figura abaixo.

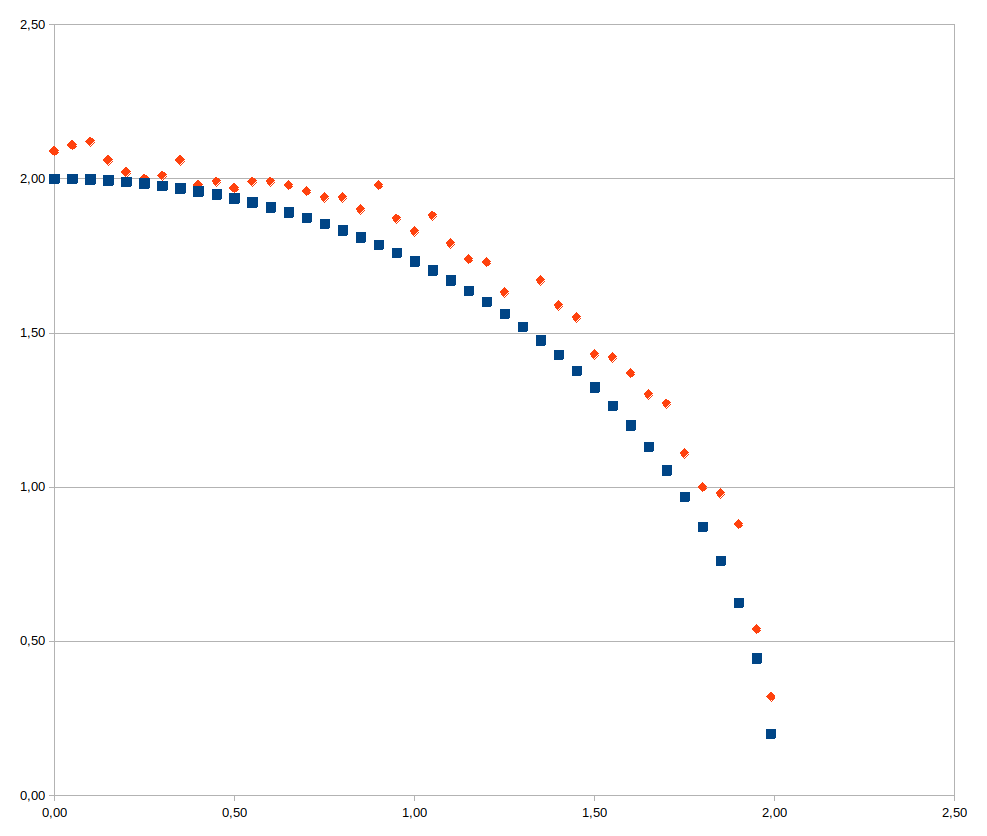
A coluna E é calculada pelo quociente entre o quadrado do resíduo e o valor ideal:

\(
\frac{(y_{ideal} – y_{real})^2}{y_{ideal}}
\)

A célula D1 contem a soma de todos os valores da coluna E e a célula D2 o valor de \( \chi^2 \) para os graus de liberdade dados por \(B1 -1\) e o nível de significancia presente na célula B2.

Observe que a estatistica \(\chi^2\) é muito próxima de zero e muito abaixo do valor \( \chi^2_{calculado} \). Assim, nossa seção escavada está muito próxima da forma da seção ideal, apesar do overbreak.

Os resíduos presentes na coluna D são, na verdade, as medidas do overbreak, ou underbreak, dependendo do sinal.

Com a coleta de dados por topografia ou scanner por exemplo, podemos, através destes dados, obter estatisticas que nos mostram o quão próximo estamos da seção ideal.
Poderíamos desenvolver aqui melhor este tópico, mas ficaria um texto longo. Em outra oportunidade retorno com este assunto e montaremos juntos um banco de dados relacional para receber e tratar estes dados.

Abraço.