A alguns anos atrás eu e o Jacopo conversávamos sobre modelagem e controle de flyrock. Se você não sabe, flyrock é o termo usual da industria para o que nós brasileiros chamamos de ultralançamento. Ao final da conversa não chegamos a qualquer conclusão decente sobre o assunto. Mas um detalhe interessante que eu lembro é que o Jacopo me mostrou um Blues intitulado Flyrock Blues. Nem preciso dizer que a música fala sobre flyrock. Você pode ouvi-la aqui no youtube. Um dos trechos mais icônicos da letra é este:
People praying “Don’t you land on me,
Flyrock Blues · Ben Sollee · Daniel Martin Moore
Don’t you bust my house. Just let me be
On my own ground”
Depois que o flyrock ocorre tudo o que resta é rezar “Don’t you land on me…”. Assim como eu e o Jacopo na nossa pequena tertúlia sobre o assunto, também as pesquisas atuais não jogam muita luz sobre o assunto. Isso porque é muito difícil prever o comportamento de um fragmento de rocha lançado sem controle de um desmonte.
A grosso modo existem duas frentes de batalha na tentativa de compreensão do flyrock. Uma utiliza uma abordagem analítica, modelando equações baseadas em princípios físicos, como impulso, conservação de momento, lançamento de projéteis e etc. A outra, opera no mundo da estatística multivariada junto com técnicas de soft computing. Modelos ANFIS (Adaptive Neuro-Fuzzy Inference Systems) começam a surgir como ferramentas para previsão e controle de flyrock.
O problema da abordagem analítica é que a modelagem do fenômeno é muito complicada. As incertezas sobre as condições iniciais, como tamanho e forma do fragmento, velocidade inicial, angulo de ejeção e outras geram modelos não muito precisos.
A segunda abordagem parece ser a mais promissora, mas tem a grande desvantagem de precisar de muitos dados. Qualquer sistema que seja baseado em redes neurais artificiais, como os modelos ANFIS, precisa de muitos, muitos dados prévios do problema estudado para ser efetivo. Estes dados servem para o treinamento e teste da rede neural artificial. Sem dados, sem previsão, ou uma saída não muito confiável. Não existem muitos dados sobre flyrock disponíveis, pelo menos na quantidade necessária para a configuração de uma ANN.
Os modelos analíticos ainda são os campeões. Vendem bem, mas quem compra precisa tomar cuidado para não confiar cegamente nos outputs; como eu disse, a modelagem de flyrock é muito difícil.
Para dificultar um pouco mais, as fontes de flyrock são diversas e cada uma requer uma abordagem particular. O ultralançamento oriundo da face de bancada pode ter muitas causas: burden insuficiente, ocorrências geológicas e desvio da perfuração são algumas.
Já o flyrock que nasce da zona de tampão pode ter outras raízes: erro de sequênciamento, overburden, comprimento de tampão insuficiente e ocorrências geológicas desfavoráveis.
Um dos modelos mais famosos de previsão de flyrock da zona de tampão é o modelo de McKenzie. Se não me engano surgiu primeiramente em um artigo chamado Flyrock Range & Fragment Size Prediction, publicado em 2009 na ISEE. As conclusões de McKenzie foram retiradas do seu artigo e transplantadas para o capitulo que fala sobre flyrock no Blaster’s Handbook, publicado pela ISEE.
Neste modelo, o alcance previsto de flyrock depende do diâmetro dos furos e da Scaled Depth of Burial – SDoB.
É melhor abrir um parenteses para explicar esta última.
Eu não conheço uma tradução para o português de SDoB. Se eu fosse traduzir, diria que é algo como profundidade escalonada. Para entender o significado prático da SDoB veja a sequência de imagens abaixo.
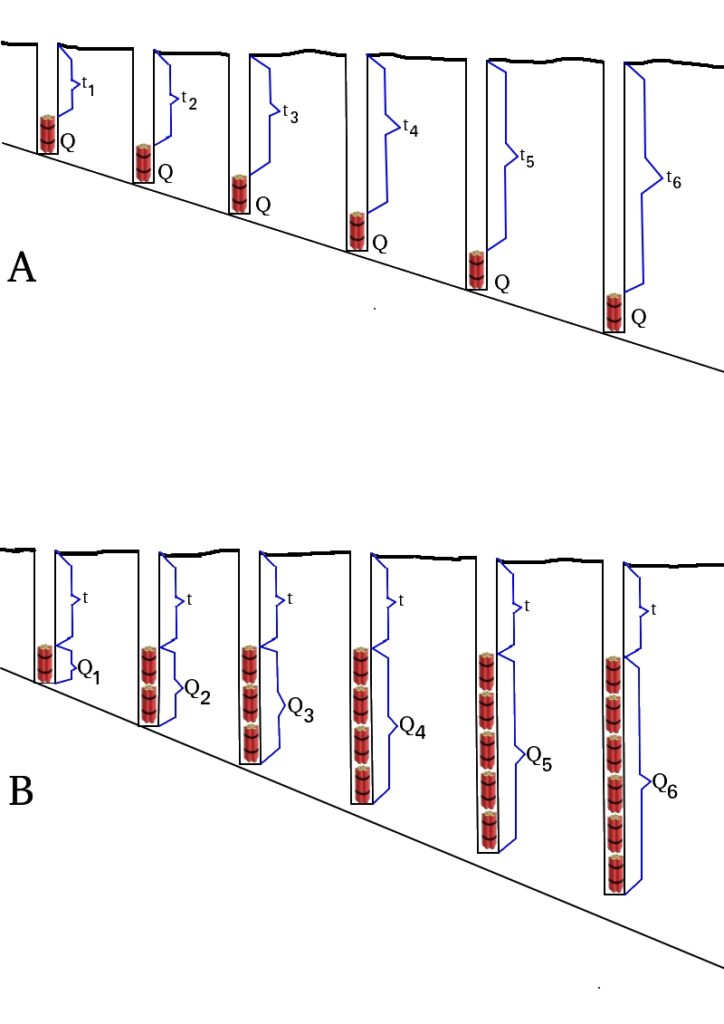
Na figura A mantemos a carga constante (Q) enquanto vamos aumentando a altura do tampão. Para cada configuração \((Q,t_n)\) medimos as configurações da cratera resultante da detonação. Diâmetro, profundidade, volume de material dentro da cratera são algumas das variáveis medidas. Chegaremos num ponto em que não haverá mais formação de cratera alguma.
Na figura B mantemos um tampão constante \(t\). Sabemos o resultado esperado para o tampão \(t\) e a carga \(Q\), então vamos aumentando a carga explosiva e observamos se isto ocasiona alterações na cratera. Chegará um ponto onde o aumento de \(Q\) não produzirá qualquer alteração na formação da cratera.
Repetimos o procedimento acima para diversos diâmetros. Destes experimentos o pessoal observou que não é todo o comprimento da caga explosiva que influencia na formação da cratera. Segundo o paper de McKenzie e o Blaster’s Handbook, para diâmetros menores que 100mm apenas o comprimento de até 8 diâmetros influencia no crateramento. Para diâmetros maiores que 100mm este valor é de 10 diâmetros. O pessoal chamou esta relação de M. Assim:
\(M \leq8 \,\,\,\, para\, D<100mm
\\
M \leq 10 \,\,\,\,para\, D \geq 100mm\)
A SDoB é a relação que existe entre o crateramento e as variáveis diâmetro do furo, tampão e comprimento da carga explosiva. Esta relação não é linear e é dada por
\(
SDoB = \frac{t+\frac{MD}{2}}{(MD\lambda)^{\frac{1}{3}}}
\)
Em que:
t = tampão.
D = Diâmetro do furo.
\(\lambda\) = Densidade linear de carregamento.
M = constante de influência da altura da carga explosiva (alguns chamam de fator de aproximação de carga esférica).
A relação \(mD\) representa o comprimento da carga explosiva que tem influência no crateramento. Assim, no numerador temos o comprimento do tampão mais a metade do comprimento da carga de influência. No denominador temos a carga explosiva associada ao comprimento de influência no crateramento elevada a potência \(\frac{1}{3}\), ou a raiz cúbica, se você preferir.
A relação teórica entre os valores da SDoB e o resultado do crateramento é mostrado na figura abaixo
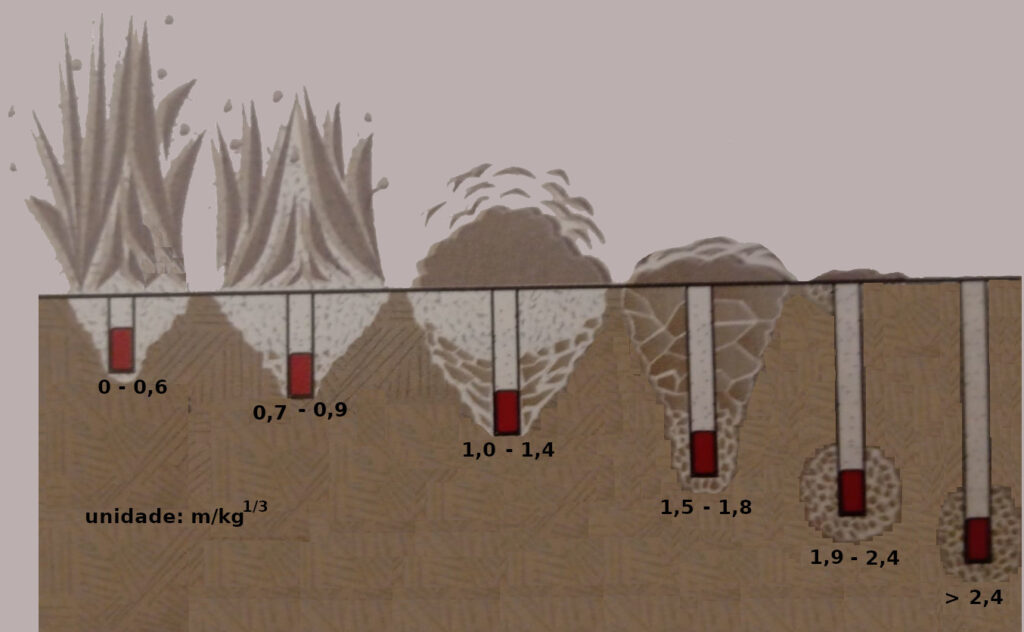
Segundo o Blaster’s Handbook, podemos classificar os intervalos em:
0 – 0,9 -> Flyrock excessivo, elevada sobrepressão acústica e ruído. O material é lançado de maneira descontrolada para fora da cratera.
1,0 – 1,4 -> Fragmentação aceitável. Baixa probabilidade de flyrock. Bom grau de confinamento. Geralmente nesta faixa de valores é onde se consegue o maior volume de material na cratera.
1,5 – 1,8 -> O volume de material empolado é bem reduzido. Baixíssima probabilidade de flyrock. A fragmentação é bem reduzida.
1,9 – 2,4 -> A fragmentação na superfície é muito pequena.
> 2,4 -> Nenhum efeito significativo na superfície.
Em algumas publicações você pode encontrar valores ligeiramente diferentes, mas grosso modo os valores estarão próximos a estes. Perceba que o pessoal da ISEE trabalha com 1 algarismo significativo após a virgula.
O alcance máximo de fragmento do modelo ISEE-McKenzie é
\(
R_{max}=11\,SDoB^{-2,167}D^{0,667}
\)
\(R_{max}\) = Alcance máximo de fragmento em metros.
\(SDoB\) = Scaled Depth of Burial em \(m.kg^{-\frac{1}{3}}\).
\(D\) = Diâmetro do furo em mm.
Tome cuidado com as unidades se você for usar este modelo. Eu não sou muito adepto dessa salada de frutas com unidades. Já vi muitas publicações onde se “corrige” a saída com a adoção de um coeficiente. Neste caso, a entrada do diâmetro é em milímetros, mas as outras variáveis obedecem o SI. Este tipo de abordagem faz com que você deva sempre se lembrar que a entrada do diâmetro é em milímetros. Se todas as variáveis estão no mesmo sistema de unidades, seja SI ou Imperial, evitam-se possíveis problemas, como o usuário da equação precisar sempre se lembrar que a entrada do diâmetro deve ser em milímetros. Essa confusão de unidades é muito comum nos papers sobre desmonte e deveria ser evitada. Parece que isso é uma prática comum dos irmãos do norte.
Os detalhes da dedução algébrica você pode conferir no paper de McKenzie ou no Blaster’s Handbook.
Veja que este é um modelo “e se…”. Ele não diz que haverá flyrock, mas, se houver, então o alcance estimado será aquele fornecido pela equação.
Existem algumas armadilhas que devem ser evitadas quando do calculo da SDoB.
Vamos alterar a forma da equação. A variável \(\lambda\) pode ser expressa como
\(
\rho = \frac{m}{V}
\\
\rho = \frac{m}{\pi\bigl(\frac{D}{2}\bigr)^2h}
\\
\rho = \frac{4m}{\pi D^2 h}
\\
\rho = \frac{4}{\pi D^2}\frac{m}{h}
\\
\frac{m}{h}=\frac{\rho \pi D^2}{4} = \lambda
\)
Acima temos
\(\rho\) = Densidade de massa efetiva do explosivo.
\(V\) = Volume de furo ocupado pelo explosivo.
\(m\) = Massa de explosivo que ocupa o volume \(V\).
\(D\) = Diâmetro do furo.
\(h\) = Altura da carga referente ao volume \(V\).
\(\lambda\) = Densidade de carregamento. Massa de explosivo por unidade de comprimento do furo.
Vamos agregar a equação acima na definição de SDoB
\(
SDoB = \frac{t+\frac{MD}{2}}{(MD\lambda)^{\frac{1}{3}}}
= \frac{t+\frac{MD}{2}}{\bigl(\frac{M \rho \pi D^3}{4} \bigr)^{\frac{1}{3}}}
= \frac{t+\frac{MD}{2}}{D\bigl(\frac{M \rho \pi}{4} \bigr)^{\frac{1}{3}}}
= \frac{\not D\bigl(\frac{t}{D}+\frac{M}{2}\bigr)}{\not D\bigl(\frac{M \pi}{4} \rho \bigr)^{\frac{1}{3}}}
\\
= \frac{\bigl(\frac{t}{D}+\frac{M}{2}\bigr)}{\bigl(\frac{M \pi}{4} \rho \bigr)^{\frac{1}{3}}} = SDoB
\)
Veja que a densidade de massa efetiva é a única variável que fornece a unidade para a SDoB, \(mkg^{-\frac{1}{3}}\).
A compreensão do termo \(\rho\) é fundamental. É ele a maior fonte de incerteza do modelo. Seu intervalo de valores válidos pode mudar dependendo do tipo de explosivo.
Para os derramados da família do ANFO, \(\rho\) pode ser igualado a densidade de massa do explosivo sem maiores problemas.
Para emulsão bombeada gaseificada quimicamente, o valor de \(\rho\) é aquele que você colhe das amostras. A densidade medida nas amostras é provavelmente a densidade de massa do explosivo próximo ao tampão. No fundo do furo a densidade de massa é maior. A emulsão bombeada com gaseificação química não é incompressível. Sua densidade varia com a altura do furo, diminuindo do pé para a crista. A densidade que você mede durante a amostragem corresponde àquela próxima ao tampão. E aqui cabe um pequeno parenteses: não invente teorias sobre qual a melhor densidade para tal rocha ou situação. Siga a orientação do fabricante que vai te indicar qual densidade de copo (amostra) você deve trabalhar em função da altura do furo. Seguir a tabela do fabricante vai te impedir de deixar a massa no fundo do furo com uma densidade muito alta, comprometendo a iniciação da coluna, além disso, seguir a orientação dos caras que fabricam a emulsão vai te proporcionar a melhor eficiência energética do explosivo.
Para explosivos encartuchados, particularmente as emulsões, a análise de \(\rho\) é um pouquinho mais complicada. Isto porque o acoplamento entre o cartucho explosivo e o furo pode pode alterar significativamente o valor de \(\rho\).
A equação que mostramos acima
\(
\frac{m}{h}=\frac{\rho \pi D^2}{4}
\)
pode ser usada para encontrar o valor mínimo da altura dentro do furo que um cartucho pode ocupar. E porque isso é importante? Por que a altura mínima junto com a máxima mapeiam a densidade efetiva que o encartuchado pode ter para o diâmetro do furo. Eu percebo que este assunto é particularmente difícil de ser entendido pelas pessoas que nunca, ou poucas vezes, carregaram um furo com encartuchado. Mas o fato é que o comprimento de um cartucho dentro do furo vai depender de alguns fatores como:
– Presença de água.
– Grau de adensamento.
– Diâmetro do furo.
– Densidade do explosivo.
– Massa de explosivo contida no cartucho.
veja que o comprimento mínimo do cartucho (\(h_{min}\)) é dado por
\(
h_{min}=\frac{4m}{\rho \pi D^2}
\)
O valor de \(h_{min}\) corresponde ao menor valor possível para o comprimento do cartucho dentro de um furo com diâmetro \(D\). Ele representa algo como se você retirasse toda a massa de explosivo do cartucho e a colocasse dentro do furo. Esta massa ocuparia uma altura \(h_{min}\).
E o comprimento máximo do cartucho, \(h_{max}\)? Será aquele que presente no catálogo. A menos que você estique o cartucho. Na verdade, ambos os extremos, mínimo e máximo, tem associada uma probabilidade de ocorrência que depende das condições particulares de cada furo.
Agora que o comprimento de um cartucho não é uma constante, a densidade efetiva torna-se uma função, também, desta nova variável.
\(
\rho \rightarrow \rho(h,D,m)
\\
\rho(h,D,m) = \frac{4m}{ \pi D^2 h}
\)
A densidade efetiva para condições particulares de diâmetro do furo e a massa explosiva presente no cartucho varia entre os valores
\(
\rho_{max} = \frac{4m}{ \pi D^2 h_{min}}
\\
\rho_{min} = \frac{4m}{ \pi D^2 h_{max}}
\)
Que é o equivalente a variação da densidade de carregamento (\(\lambda\)):
\(
\lambda_{max} = \frac{m}{h_{min}}
\\
\lambda_{min} = \frac{m}{h_{max}}
\)
Você pode combinar as duas equações e formar:
\(
\rho_{max} = \frac{4}{ \pi D^2}\lambda_{max}
\\
\rho_{min} = \frac{4}{ \pi D^2 }\lambda_{min}
\)
Um exemplo. Para um furo de 3″ (0,076m) de diâmetro, utilizando um cartucho de 2 1/4″ (0,05715m) de diâmetro e comprimento de 24″ (0,61m), cuja massa de explosivos é de 1,56kg e a densidade de massa é 1150kg/m³, teremos:
\(
h_{min}=\frac{(4)\,(1,56)}{(1150) (3,141592) (0,076)^2} = 0,30m
\\
h_{max} = 0,61m
\\
\rho_{max} = 1150kg/m^3
\\
\rho_{min} = \frac{(4)(1,56)}{ (3,141592) (0,076)^2 (0,61)} = 564kg/m³.
\\
\lambda_{max} = \frac{1,56}{0,30} = 5,2kg/m
\\
\lambda_{min} = \frac{1,56}{0,61} = 2,56kg/m
\)
Veja que existe uma grande variação na densidade efetiva e consequentemente na densidade linear de carga. Isso causa alguns inconvenientes para a SDoB:
1 – A SDoB não foi definida levando-se em consideração os efeitos do desacoplamento da carga explosiva. Ou seja, não se pode afirmar que manterá a amplitude dos efeitos esperados para densidades efetivas menores que a densidade de massa do explosivo.
2 – Pode ser difícil prever um valor aproximadamente exato para a SDoB quando se utiliza explosivos encartuchados. Isso pode acarretar em valores teóricos incorretos, ocasionando um potencial elevado de flyrock, ou, pelo outro lado, conduzir a um desmonte excessivamente confinado.
Com os valores numéricos acima, se você utilizar a densidade de massa do explosivo como parâmetro para a SDoB, isto é \(\rho = 1150\), para um tampão hipotético de 1,5m você vai obter:
\(
SDoB = \frac{\frac{1,5}{0,076}+\frac{8}{2}}{\frac{8\pi}{4}1150}=1,23m.kg^{-\frac{1}{3}}
\)
Agora, se a densidade efetiva se aproxima do outro extremo, por causa da presença de água nos furo, por exemplo, então
\(
SDoB = \frac{\frac{1,5}{0,076}+\frac{8}{2}}{\frac{8\pi}{4}564kg}=1,56m.kg^{-\frac{1}{3}}
\)
Compare estes dois valores com o intervalo de valores da SDoB presentes na figura acima.
A melhor maneira de enfrentar estas perturbações no modelo é não ignorar as incertezas, mas tratá-las.
Você pode, por exemplo, supor que qualquer valor no intervalo \([\rho_{min};\rho_{max}]\) possui a mesma probabilidade de ocorrência. Assim
\(
\frac{\bigl(\frac{t}{D}+\frac{M}{2}\bigr)}{\bigl(\frac{M \pi}{4} \rho_{max} \bigr)^{\frac{1}{3}}} \leq SDoB \leq \frac{\bigl(\frac{t}{D}+\frac{M}{2}\bigr)}{\bigl(\frac{M \pi}{4} \rho_{min} \bigr)^{\frac{1}{3}}}
\)
Adicionando também um variação no diâmetro \(0,069m \leq D \leq 0,076m\) e no tampão \(1,40m \leq t \leq 1,60m\) obtemos os dois histogramas:
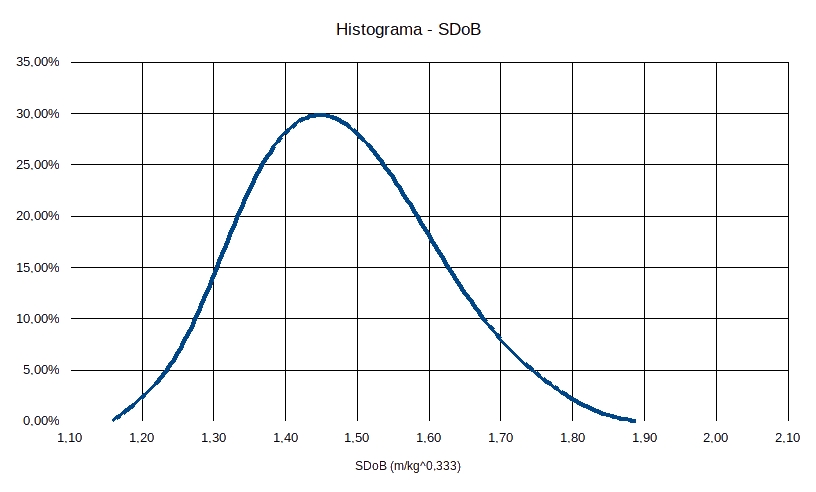
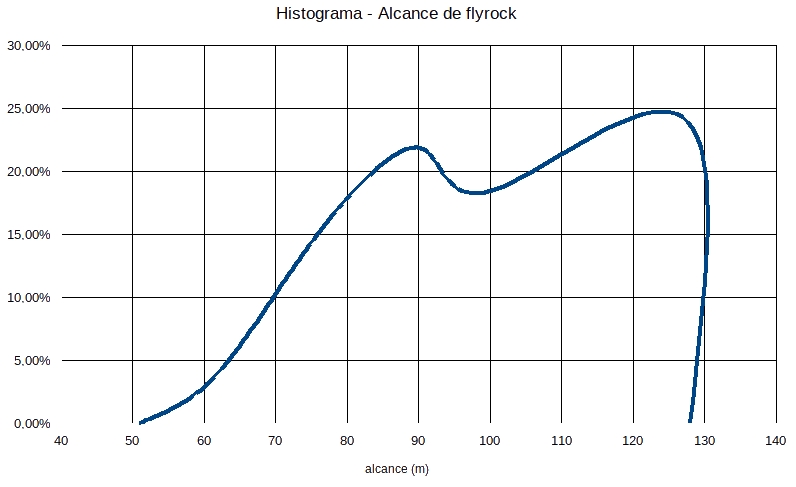
O número de simulações foi de 10321. Talvez com o aumento deste número o histograma do alcance de flyrock tenda a uma normal bem definida.
Algumas informações que podemos retirar destes dois gráficos são:
1 – Pode ser que exista uma grande chance (95%) do alcance teórico de flyrock permanecer no intervalo [70m;128m]
2 – Existe uma probabilidade teórica de \(\approx 30\%\) de que ocorra uma fragmentação não muito boa na zona de tampão (\(SDoB > 1,5)
Obviamente isso são suposições, mas também são um indicativo do caminho a seguir se o objetivo é refinar o projeto de desmonte mantendo o flyrock sob controle.
É muito provável que a distribuição dos valores da densidade efetiva obedeça uma distribuição outra que uma distribuição uniforme. Talvez uma log-normal seja mais indicada à simulação. Enfim, o objetivo aqui não é exaurir o assunto, mas lhe fornecer um passo inicial para você fazer as suas próprias simulações.
Um ultimo aviso: sempre adicione um coeficiente de segurança em qualquer modelo teórico de previsão de flyrock. Um regra comum que muitos usam é multiplicar o valor máximo de alcance de flyrock por 5. Por exemplo, na simulação acima teríamos para um raio de isolamento:
\(R_i =128m x 5 = 640m\)
Sempre mantenha seus desmontes dentro de um envelope de segurança que contenha pelos menos os dois pilares básicos de segurança:
– Controle de flyrock.
– Controle de vibrações.
Até a próxima!

Estimados, excelente trabajo.
Quisiera comentar que he observado en diferentes yacimientos, la falta de control en perforación y otras mediciones. Los tiempos y exigencias de producción muchas veces dejan de lado aspectos que parecen no tener importancia pero luego se traducen en mayores costos y deficiencia en la seguridad.