No campo de pesquisa do desmonte de rochas existem muitos troféus avidamente perseguidos. Certamente, um dos mais cobiçados é a teoria definitiva do desmonte de perímetro, ou contorno, ou linha de escavação, como você preferir chamar. Muitas técnicas já foram desenvolvidas. Metodologias como pre-splitting, smooth blasting, trim blasting e line drilling são as mais famosas. O Santo Graal desta área de pesquisa é encontrar um modelo universal que faça a previsão correta do resultado final. Quem já esteve lá na linha de frente sabe como é muito frustrante ver que muitas vezes as técnicas de corte escultural não funcionam adequadamente. Se você procurar por aí vai ver que existem muitas, digamos, “regrinhas práticas” e muito ruído a respeito. Toda a informação que cerca o assunto daria facilmente uma enciclopédia de mitos e lendas. Mas também tem o outro lado. A piazada que tenta entender o assunto e desenvolver maneiras de ajudar na obtenção de um corte bonito e estável na parede final. Uma das abordagens que essa galera usa é a busca do entendimento de até onde a influência da carga explosiva altera a resistência da rocha. Colocando de uma maneira mais simples, até onde vão as fissuras e trincas induzidas pela ação dos explosivos, mesmo aquelas imperceptíveis, mas que alteram o conjunto de resistências da rocha? Sabendo dessa informação, o objetivo é colocar os furos em distâncias adequadas à parede final de maneira que não produzam efeitos negativos nos limites da escavação. Como se a linha de escavação fosse sua filha e você quer que ela não receba a influência das más companhias dos furos com explosivos perto dela.
Na minha opinião, ainda estamos bem longe da perfeição para os modelos de previsão de dano. Talvez a abordagem analítica para um modelo universal não seja nem mesmo possível. O que isso quer dizer? Que provavelmente não exista uma equação, ou um conjunto de, que possa formular o fenômeno de uma maneira razoável, pelo menos.
Vou te mostrar dois modelos que são muito usados. O modelo de Holmberg e o modelo da gurizada do NIOSH. Estas duas abordagens foram desenvolvidas primariamente para ajudar na obtenção de contornos mais regulares e estáveis em túneis e galerias. Existem muitas outras, mas estas duas ainda são muito usadas e ensinadas. Já deixo aqui algumas observações. Eu tenho ressalvas quanto algumas questões metodológicas que foram aplicadas no desenvolvimento que foi adotado. Estas minhas observações não tentam invalidar os modelos ou coisa parecida. Longe disso, considero eles muito producentes e práticos quando adotados de uma maneira pragmática, conforme veremos.
Começamos com o modelo de Holmberg. Você pode encontrar a dedução e o texto original no célebre livro Rock Blasting and Explosives Engineering. Este livro foi escrito por três caras: Holmberg, Persson e Lee. Mas eu vou me referir neste texto como modelo de Holmberg apenas, para facilitar. O livro é uma boa leitura, recomendo.
No modelo de Holmberg é utilizada a linha clássica de pensamento que associa o potencial de dano ao meio circundante da carga explosiva confinada em um furo a velocidade de partícula induzida. Holmberg faz uso da equação
\[PPV=k\frac{Q^{\alpha}}{R^{\beta}}\]
Nela, \(PPV\) é o módulo (preste atenção, módulo) da velocidade de pico de partícula. \(Q\) é a carga explosiva que teoricamente gera a \(PPV\) e \(R\) é a distância entre o ponto onde ocorre a \(PPV\) e o centro da carga \(Q\). Veja que aqui não estamos falando de CME (Carga Máxima por Espera), mas de uma única carga explosiva dentro de um furo. Os parâmetros \(k\,,\alpha\) e \(\beta\) serão explicados adiante. Por enquanto, repare que estamos lidando com distâncias radiais. No caso \(PPV = constante\) forma uma curva de nível. Para uma mesma carga explosiva \(Q\) a \(PPV\) depende apenas da distância \(R\). Isso vai conduzir a curvas de níveis circulares que contem o mesmo valor de \(PPV\). Da uma olhadinha na figura abaixo.
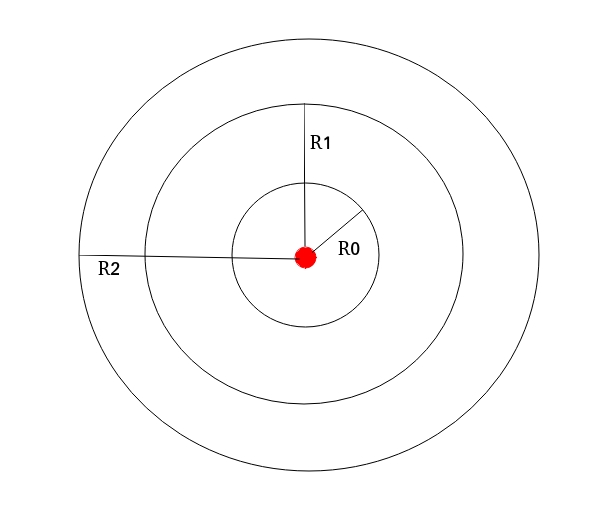
Cada circunferência de raio \(R_n\) representa, em um mundo ideal, regiões a partir da carga em vermelho onde a velocidade de partícula é constante. Mas se você tá ligado, não dá pra usar essa simplificação no caso de cargas explosivas confinadas em um furo. O pessoal percebeu que a carga explosiva não é um ponto, mas uma distribuição de carga ao longo de um furo. Assim, a equação da \(PPV\) acima deve ser considerada para cada elemento infenitesimal de carga no furo. Holmberg desenvolve o modelo baseado nas hipóteses consideradas na figura abaixo.
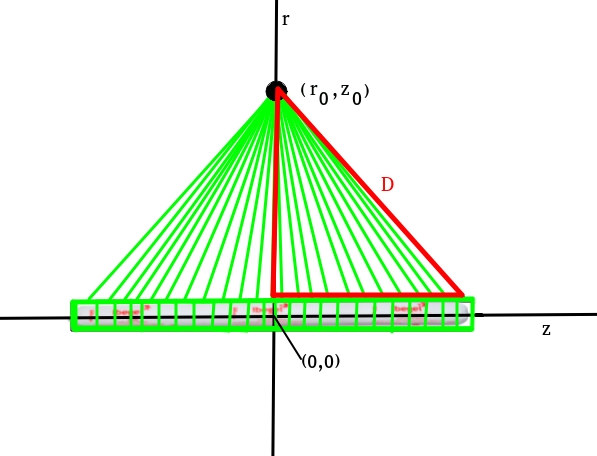
Cada retângulo verde representa uma parte do cartucho explosivo que contribui para a \( PPV \) no ponto \( (r_0,z_0) \). Assumindo que a massa de explosivo por comprimento é constante e igual a \(q\), podemos dizer que cada pequeno retângulo tem uma massa de explosivo dado por:
\[ m_n=q\Delta z \]
Você lê a equação acima assim: \(m_n\) é a massa associada a o n-ésimo elemento, \( \Delta z \) é o comprimento ao longo do eixo \(z\) dos elementos. O passo a seguir é substituir a massa \(Q\) na equação da \( PPV \) pela massa \(m_n\).
\[PPV_n=k\frac{(q\Delta z)^{\alpha}}{R^{\beta}}\]
Veja que a equação acima representa a contribuição para a \(PPV\) de um dos elementos. Agora, a distância de cada elemento ao ponto \( (r_0,z_0) \), que na figura é representada por \(D\), é dada por:
\[ D = \sqrt{(z_n^2 + r_0^2)} \]
Uma vez que \(z_0 = 0\). A equação da PPV fica então:
\[PPV_n=k \frac{ (q\Delta z)^{\alpha} } { (z_n^2 + r_0^2) ^{ \frac{\beta} {2} } }\]
E a partir daqui começou a peleia. Holmberg prosseguiu da seguinte forma, fazendo os pequenos retângulos cada vez menores, ou ainda, fazendo seu comprimento ao longo do eixo \(z\) tender a zero, transformando a soma
\[ \sum_0^n PPV_n = \sum_0^n \frac{ k(q\Delta z)^{\alpha} } { (z_n^2 + r_0^2) ^{ \frac{\beta} {2} } } \label{eq1} \]
na integral
\[ \int_{z_i}^{z_f} PPV = \int_{z_i}^{z_f} \frac{ k(q dz)^{\alpha} } { (z^2 + r_0^2) ^{ \frac{\beta} {2} } } \]
considerando que quando você faz muitos retângulozinhos verdes, ou seja, \( n \rightarrow \infty \), a medida de um dos lados deles, \( \Delta z \), tende a zero, \(\Delta z \rightarrow 0\ \), daí podemos substituir \( \Delta z \) por \(dz\). Na verdade, a explicação é um pouco mais profunda, envolve o conceito de diferencias, mas o pessoal do rigor matemático vai me perdoar, com certeza.
Você precisa ser uma mistura de Santa Maria Madalena, Chuck Norris e Fredie Mercury pra encontrar uma solução analítica para a integral acima. A solução numérica também é complicada, aquele \(\alpha\) como expoente da diferencial \(dz\) não torna as coisas fáceis. Não me pergunte o motivo, mas o pessoal tentou uma gambiarra. Sem qualquer pudor jogou o expoente \(\alpha\) para fora do integrando, assim
\[ \int_{z_i}^{z_f} PPV = k \left( \int_{z_i}^{z_f} \frac{q dz } { (z^2 + r_0^2) ^{ \frac{\beta} {2\alpha} } }\right)^{\alpha} \]
Isso está errado pessoal. Não dá para progredir no passo acima sem assassinar o teorema fundamental do calculo. A intenção era, ao que parece, tornar possível a resolução da integral dentro dos parenteses. Quem aparentemente apontou este erro no modelo de Holmberg foram dois caras, Hustrulid e Lee, em um paper escrito para o Fragblast em 2002 intitulado Some General Design Concepts Regarding the Control of Blast-Induced Damage During Rock Slope Excavation.
Em um outro paper, Application of the NIOSH-Modified Holmberg-Persson Approach to Perimeter Blast Design, escrito pela galera do NIOSH, é apresentada uma linha alternativa, mas ainda baseada no desenvolvimento inicial de Holmberg.
Esta outra abordagem tem mais ou menos as seguintes premissas.
1) OK, esqueçam as contribuições infinitesimais de massa dos elementos de carga. Vamos considerar a carga completa, \(q(z_f – z_0) = qL\).
2) Vamos considerar o raio médio de todos os elementos que contribuem para a PPV, assim
\[r_m = \frac{1}{L}\int_{z_i}^{z_f}\left(z^2+ r_0^2\right)^\frac{1}{2}dz \]
A nova roupagem da \(PPV\) fica
\[PPV = \frac{k (qL)^\alpha}{\left(\frac{1}{L}\int_{z_i}^{z_f}\left(z^2+ r_0^2\right)^\frac{1}{2}dz\right)^\beta} \]
Tanto na abordagem de Holmberg quanto no NIOSH são assumidas duas considerações inicias:
1 – A PPV é dada somente pela soma das contribuições de cada elemento de carga.
2 – A carga explosiva detona instantaneamente, ou seja, não existe um ponto de iniciação em que a detonação começa a se desenvolver.
A integral no denominador da expressão acima é um pouco mais palatável. Tem solução analítica relativamente simples.
\[\int_{z_i}^{z_f} (z^2+ r_0^2)^\frac{1}{2}dz = \\
=\frac{1}{2} \left(z \sqrt{(r_0^2 + z^2)} + r_0^2 \ln{ \left( \sqrt{(r_0^2 + z^2) } + z \right)} \right)\biggl|_{z_i}^{z_f}\]
Com este modelo podemos avaliar a expressão para diversos comprimentos de carga (\(z_f-z_i)\), massa de explosivos por comprimento de furo (\(q)\) e distância do ponto considerado, (\(r_0)\), resultando em gráficos como o mostrado abaixo.
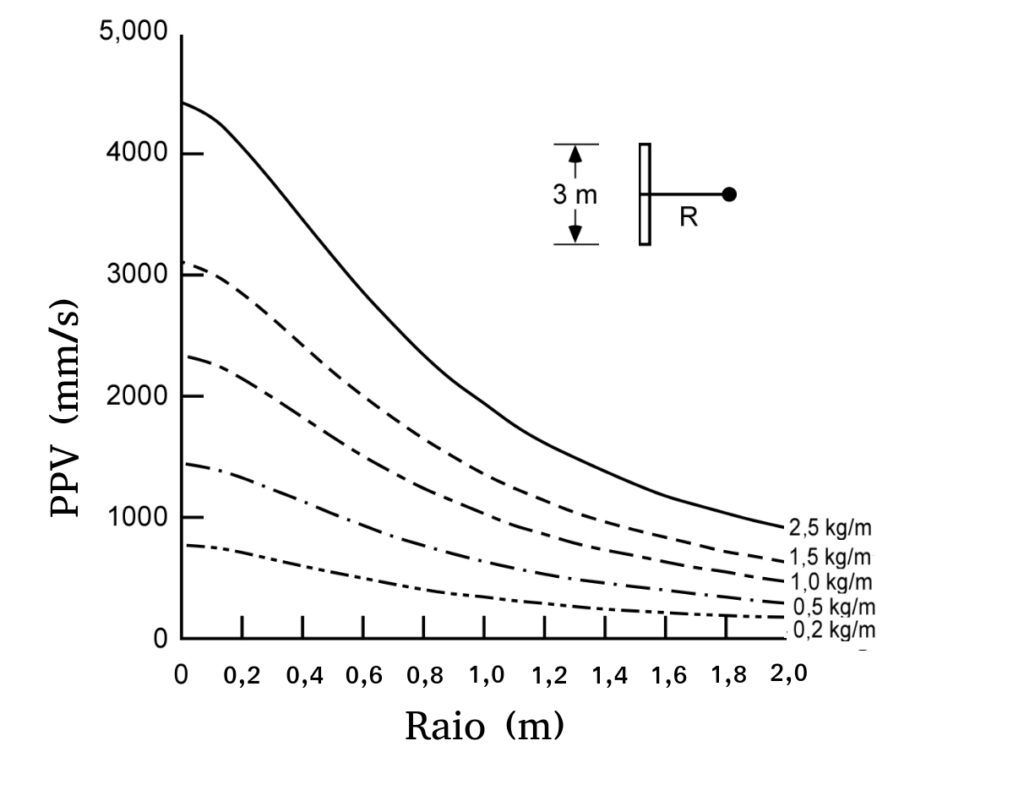
Este gráfico eu adaptei do paper do NIOSH, Application of the NIOSH-Modified Holmberg-Persson Approach to Perimeter Blast Design citado acima no texto.
E a ideia é que, se você sabe qual é a PPV crítica na sua situação, você consegue saber a distância que deve manter suas cargas explosivas do seu ponto de controle. Por exemplo, se seu limite de velocidade é de \(1000mm/s\) você deve deixar os furos com carga explosiva a distâncias superiores as informadas no gráfico abaixo, para cada curva de densidade linear de carga.
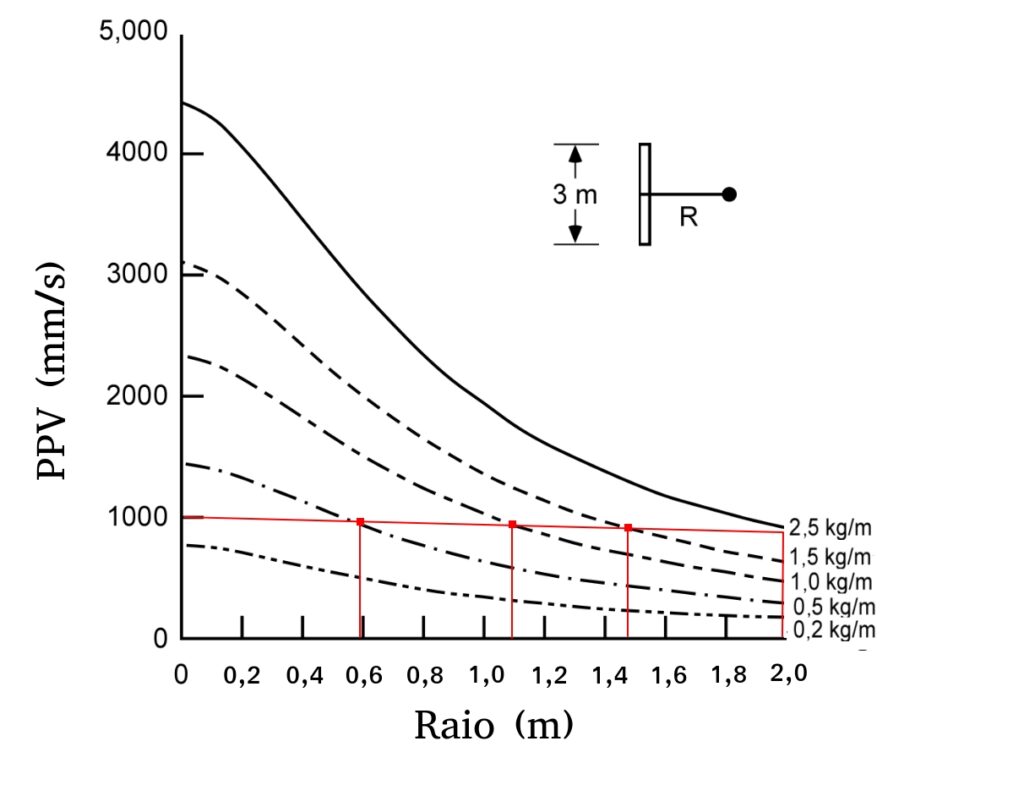
Mas como construímos estes gráficos? Como obter os coeficientes \(\alpha\,,\,\beta\) e \(k\)?
Você provavelmente notou que a equação da PPV usada nos modelos acima não é exatamente igual àquela que o povo usa na previsão de vibrações. Nesta última uma estratégia de linearização dos dados é usada, a bem conhecida transformação chamada de distância escalonada. Você deve se lembrar, dividimos a carga máxima por espera por alguma potência da distância, assim:
\[DE=\frac{CME}{D^{\beta}}\]
E por quê não se usou a equação acima nos dois modelos, de Holmberg e do NIOSH? A resposta que vou te dar é um resumo, não quero me estender muito neste detalhe senão o texto vai se desviar muito.
A curva de previsão de vibração e a estimativa de PPV para um campo próximo são modelos físicos de certa forma diferentes. Cada uma procura modelar eventos distintos. Na PPV de campo próximo estamos interessados na vibração ocasionada por cargas pontuais; no modelo de previsão de PPV para controle de vibrações estamos interessados em encontrar a curva de melhor ajuste para um conjunto de dados e as cargas explosivas são consideradas como a soma de cargas em uma mesma sequência.
Se você tentar usar a transformação da distância escalonada para campo próximo trará muito erro para a sua análise. Basicamente isso ocorre porque quando você está muito próximo da fonte, os furos que estão mais próximos ao geofone produzem muito mais vibrações do que os mais distantes, mesmo que pertençam a mesma sequência e a CME não faz muito sentido. Não estamos atrás da maior soma das cargas na mesma sequência, mas interessados na observação de todas as fontes de vibração. Ao contrário, quando você está suficientemente afastado, pode, de certa forma, considerar todos os furos de uma mesma sequência como uma carga só, daí o conceito de CME e, consequentemente, distância escalonada.
Os coeficientes \(\alpha\,,\,\beta\) e \(k\), de certa maneira, englobam mais ruídos e incertezas quanto mais longe da fonte você estiver. Isso significa que os valores de \(\alpha\,,\,\beta\) e \(k\) serão diferentes para vibrações muito próximas a fonte e de vibrações mais afastadas da fonte. Você pode pensar nos coeficientes como muito sensíveis a anisotropia do meio.
Encontrar os coeficientes para campo próximo não é tão simples. O pessoal do NIOSH teve que organizar uma verdadeira epopeia para conseguir. Eles colocaram três sismógrafos próximos aos avanços de uma galeria e extraíram a PPV de cada pico do sismograma e associaram cada pico a um furo do desmonte. Como eles conseguiram isso? Coletaram todos os picos de velocidade resultante e através do tempo de chegada, associaram a sequência o tipo e quantidade de explosivo. Isso só foi possível devido a inerente dispersão dos nã-elétricos. Caso os furos detonassem exatamente ao mesmo tempo, não seria possível considerar no sismograma os picos das cargas individuais. O pessoal não dá muito detalhes desta parte do experimento, você pode conferir diretamente no paper deles. Mas o fato é que mantendo as cargas constantes para todos os furos e conhecendo as distâncias do geofone até o centro geométrico das cargas explosivas, você pode usar a seguinte estratégia para obter \(\alpha\,,\,\beta\) e \(k\):
- Linearizar a equação.
\[ \ln(PPV) = \ln\left( \frac{kQ^{\alpha}}{R^{\beta}} \right)
\\
\ln(PPV) = \ln(k)+\alpha\ln(Q) – \beta\ln(R)
\]
2. Observe que utilizando valores constantes para \(Q\) e \(R\) você pode encontrar \(\alpha\) como a inclinação da reta \(P \rightarrow P(B)\) quando \(R\) é constante:
\[ P = A + \alpha B – C \]
e \(\beta\) como a inclinação da reta \(P \rightarrow P(C)\) quando \(Q\) é constante:
\[ P = A + B – \beta C \]
Perceba que \( P = \ln(PPV) \), \(A = \ln(k)\), \(B = \ln(Q)\) e \(C=\ln(R)\) e que fizemos \(\beta = 1\) e \(\alpha = 1\) para encontrar os coeficientes. Isso não afeta a inclinação da reta, apenas desloca a intercepção com o eixo de \( \ln(PPV) \), mantendo os coeficientes representados pela inclinação inalterados. Desta forma, você pode usar quaisquer valores para \( (A+B) \) e \( (A-C) \) para encontrar \(\alpha\) e \(\beta\). Obviamente que você percebeu que todos eles, \(\alpha\,,\,\beta\) e \(k\) são produtos de um best fitting de uma reta, portanto, terão uma incerteza associada.
Todo este desenvolvimento acima serviria tanto para dimensionar a buffer line (também muito conhecida no Brasil como linha dos auxiliares de contorno, ou somente auxiliares) quanto a carga dos furos de contorno. A figura abaixo ilustra um exemplo de aplicação do modelo. Todos os furos que podem afetar o perímetro da escavação são colocados a distâncias tais que seu potencial dano devido a PPV gerada não ultrapasse aquele inevitavelmente gerado pelos furos do contorno.
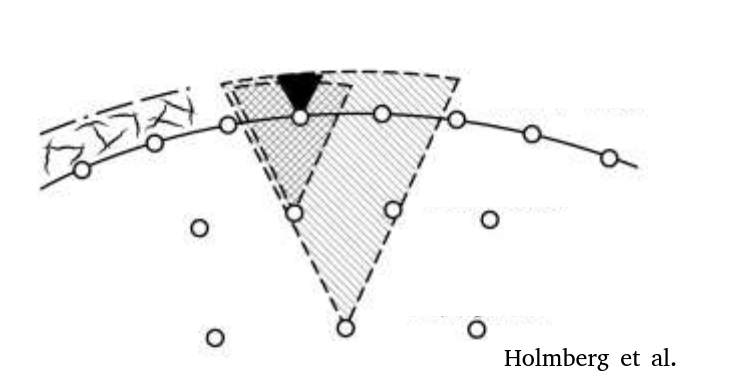
Esta figura foi retirada do RI9691.
Este modelo matemático que descrevemos até aqui não leva em consideração o tipo de explosivo, seu acoplamento no furo e os parâmetros da rocha circundante. Além disso, a relação causa-consequência entre PPV e dano é controversa.
Em 2008 dois caras, Hustrulid e Johnson, publicaram o artigo A gas pressure-based drift round blast design methodology. Este artigo foi uma das bases para o RI9691 do NIOSH. RI é a sigla para Report of Investigation, numa tradução livre, Relatório de Investigação. Neste RI é sugerida uma metodologia de cálculo para o dimensionamento da buffer line com o intuito de minimizar o efeito negativo sobre o contorno da escavação. É a mesma tentativa de Holmberg, mas com a diferença que a PPV não é o carro chefe. Neste relatório os caras introduzem um conceito chamado de practical damage radius \( (R_d) \). Eu vou reproduzir aqui ipsis litteris como eles definem \(R_d\):
A practical damage radius \((R_d)\) is determined for each blasthole/explosive combination. The damage radius calculated from the buffer holes would determine the perimeter burden. By “practical,” it is meant that if the rock mass lying outside of this ring were removed, the rock remaining within the ring would easily break apart.
Stephen R. Iverson, William A. Hustrulid, and Jeffrey C. Johnson – RI9691
A receita acima diz que o raio de dano prático, se assim podemos chamar, é uma região circundante ao furo que sofre a influência da carga explosiva de maneira que as propriedades de resistência da rocha são profundamente alteradas. Esta distância, este raio, deve ser usado para projetar o Burden da linha de contorno, deste modo espera-se que:
- Os furos da buffer line não afetem negativamente a rocha além do perímetro da escavação.
- Os furos de contorno possam facilmente remover o volume de rocha a sua frente (Burden), pois esta porção de volume foi precondicionada pelo \(R_d)\).
Este modelo propõe que a maioria do cuidado com o contorno da escavação está no dimensionamento da buffer line. Para encontrar o valor de \(R_d\) o pessoal fez uso de duas teorias, a teoria de Ash que diz que o Burden é uma função do diâmetro do furo \(D_f\):
\[B= \kappa D_f\]
E a teoria de Hustrulid sobre como a constante \(\kappa\) pode ser determinada por
\[\kappa = 25\sqrt{ \frac{ \rho_e S_{ANFO} }{ \rho_{ANFO} } } \sqrt{ \frac{2,65}{\rho_r} }\]
Os parâmetros são:
\(\rho_e\) = densidade do explosivo usado.
\(S_{ANFO}\) = RWS do explosivo em relação ao ANFO.
\(\rho_{ANFO}\) = Densidade do ANFO \((0,85g/cm^3)\).
\(\rho_r\) = Densidade da rocha.
Nos papers de Hustrulid que li eu não encontrei o desenvolvimento da equação acima. Pelo que entendi, ela surge nos livros Blasting principles for open pit mining, volume 1, 2. Como não tenho acesso aos volumes, não posso te dizer como Hustrulid chegou na equação. Fico te devendo essa. As raízes ponderando um \(\kappa\) inicial dão uma idéia, mas não posso afirmar nada. Se você souber, me envia um e-mail que publico aqui com seu nome.
Lá no RI9691 o pessoal diz que o Burden deve ser considerado como dois raios de dano, um raio para o furo a frente e outro raio para o furo em questão, isto é, a contribuição de dois furos onde as circunferências associadas ao dano de cada furo se tocam:
\[B = 2R_d\]
Combinando a equação acima com o Burden definido por Ash e observando que o o diâmetro do furo, \(D_f = 2r_f\) :
\[B= \kappa D = \kappa 2r_f = 2R_d \\
\frac{R_d}{r_f}=\kappa \\
\frac{R_d}{r_f}= 25\sqrt{ \frac{ \rho_e S_{ANFO} }{ \rho_{ANFO} } } \sqrt{ \frac{2,65}{\rho_r} }\]
Se você manja da turma dos “S” (AWS, ABS, RWS, RBS) vai perceber que
\[\frac{ \rho_e S_{ANFO} }{ \rho_{ANFO} } = RBS\]
Com isso dá pra dar uma simplificada
\[\frac{R_d}{r_f}= 25\sqrt{RBS} \sqrt{ \frac{2,65}{\rho_r}}\]
Só toma cuidado porque o RBS acima é relativo ao ANFO considerado pela gurizada do NIOSH. Pra você utilizar o ANFO padrão Brasil você vai ter que calcular o RBS do explosivo que você está usando em relação ao ANFO padrão Brasil. Não se esqueça que RBS significa Relative Bulk Strength, portanto é sempre relativo a uma medida inicial. Antigamente se usava a nitroglicerina, hoje em dia a galera migrou a turma dos “S” para o ANFO.
Este modelo é muito simples, foi pensado na galera de campo que precisa de um parâmetro rápido de ser calculado. Existem metodologias mais complexas que usam, por exemplo, a modelagem do campo de tensões induzido na vizinhança do furo. Mas ao que parece o NIOSH tentou estabelecer uma regrinha básica para o pessoal começar a se preocupar com o overbreak no perímetro da escavação e com isso diminuir a incidência de acidentes devido a queda de choco (rock fall). Mesmo que você tenha algumas divergências quanto ao desenvolvimento físico-metemático do modelo deve admitir que o motivo por trás é muito legal. Eles até desenvolveram um software para facilitar a sua vida. Você pode baixá-lo gratuitamente aqui.
As minhas pequenas considerações, que você pode livremente ignorar se quiser, sobre as abordagens de Holmberg e do NIOSH são relativas a questões implícitas nos modelos que, para mim, ficam sem reposta.
O modelo de Holmberg afirma que a PPV é totalmente responsável pelo dano. Dessa afirmação surgem questionamentos. Qual seria a PPV limite? Como considerar que a anisotropia do meio não influencia o dano? Veja, eu considero que uma abordagem mais suave deve ser usada se você quer usar este modelo. Categoricamente afirmar um limite rígido para PPV é um pouco complicado. Ainda, considerar que os coeficientes da equação são universais soa um pouco, digamos, improvável. Trabalhar como modelos fuzzy e simulações onde você coloca um grau de incerteza pode ser bem mais interessante se você quer usar este modelo.
Vamos perturbar os parâmetros do modelo NIOSH-Holmberg com os seguinte valores:
\[\kappa = 700 \pm 35 \\
\alpha = 0,5 \pm 0,025 \\
\beta = 1,5 \pm 0,075 \\
L = 3,0 \pm 0,1 \\
q = 2,0 \pm 0,1 \\
r_0 = 1,0 \pm 0,1\]
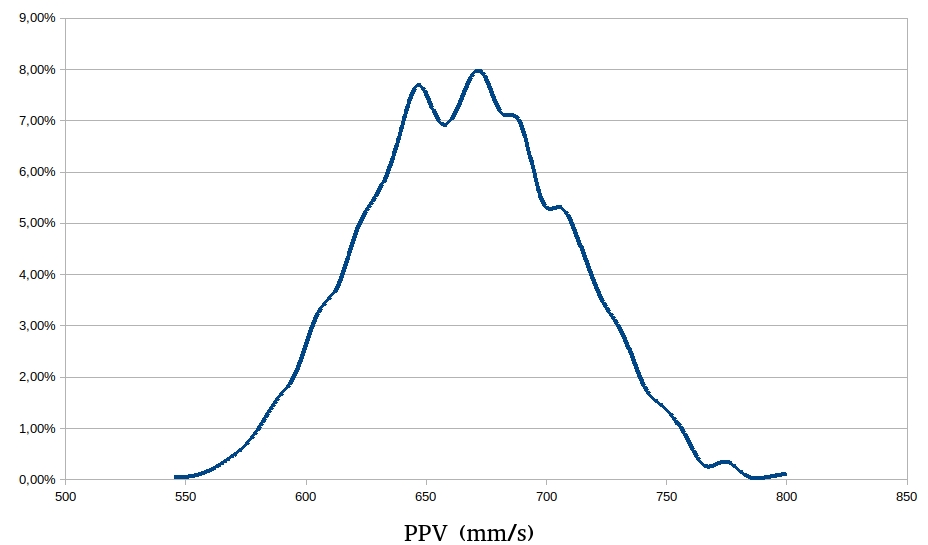
Simulando 2627 vezes o modelo com os intervalos acima dentro de uma distribuição uniforme, obtemos um histograma de PPV prevista:
A estatística descritiva obtida foi
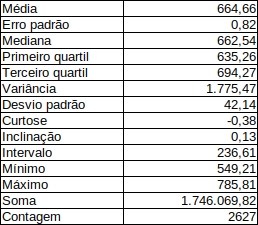
A variação dos parâmetros foi muito pequena. Nos coeficientes foi de \(5%\) e nas variáveis valores muito menores do que se fossem feitas medidas em campo. Já se percebe que um valor fixo para a previsão da PPV não é uma boa estratégia. Neste caso, você deve se perguntar se a situação na qual você está aplicando o modelo suporta estas variações na incerteza da PPV.
Mesmo para o modelo de Raio de Dano do NIOSH existem incertezas quanto aos valores de entrada, principalmente se você usar a metodologia da pressão de detonação que eles descrevem no RI.
Além disso, no estudo do NIOSH o pessoal tentou comprovar o modelo colhendo dados de 5 desmontes e realizando testes em blocos de concreto. Olha só, uma amostra com 5 desmontes é muito pequena…
Para situações críticas sempre coloque as incertezas, não as ignore. Neste desmonte abaixo, simulei o campo de tensões próximos do furo com todas as incertezas relativas a precisão da perfuração, variação do diâmetro dos furos, propriedades do concreto, carga linear de explosivos, VOD dos explosivos e muitas, muitas outras variáveis. Com isso não obtive valores exatos para a tensão que o concreto ficaria exposto, mas consegui envelopar o desmonte de modo que, mantendo as variáveis que eu podia controlar dentro de um intervalo de valores, a tensão que o concreto ficaria exposto estaria dentro de limites aceitáveis. Quando me perguntaram quais seriam os esforços que a estrutura ficaria exposta eu respondi que não tinha exatamente o número que eles buscavam saber, mas tinha certeza que não ficaria exposta a valores inaceitáveis. Foi um desmonte projetado com um viés tautológico.
Abraço!
