A teoria do desmonte de rochas esta em sua maioria apoiada em relações geométrica e algumas análises estatísticas de pequenos experimentos. Os cânones da arte de fragmentar rochas ainda não foram completamente observados. É curioso perceber que na grande maioria dos textos introdutórios não existe um paragrafo para introduzir, mesmo numa forma inquisidora ou em afirmações, a tentativa de responder a simples pergunta do porque as coisas quebram. Para mim parece inevitável que o reflexo da quebra da rocha pela ação de explosivos tem suas bases oriundas nas regras que regem o comportamento atômico, tal como na termodinâmica clássica onde as variáveis de estado refletem comportamentos microscópicos. Alguns textos tentam apontar para um possível amalgama entre a teoria da fratura, tal como a proposta por Griffith e aprimorada por outros, e a ação dos explosivos. Mas o fato é que a tentativa da junção de uma teoria físico-matemática mais elaborada ao problema do desmonte de rochas não é uma tarefa que possa conduzir de imediato a um entendimento maior do fenômeno. Existe a necessidade da confirmação em laboratório dos resultados teóricos, caso contrário, assumimos o risco de conduzir a teoria ao caos da guerra de opiniões. Muitos estudos baseados em dados não conseguem a pureza e o embasamento necessários para saltar a barreira do ad hoc. Ainda estamos longe de uma possível união da teorias mostradas na figura.
E todo este texto introdutório um pouco rebuscado é minha maneira de te avisar que o desenvolvimento matemático que vem a seguir carrega dois grandes avisos luminosos.
O primeiro é que a teoria apresentada tem seu conteúdo completamente imerso no conjunto das relações geométricas presentes na teoria do desmonte atual. Mas, o raciocínio lança alguma luz no caminho das outras teorias do outro lado da ponte.
Segundo, a matemática é a caixa de ferramentas que temos para tentar entender o universo. Entendê-la é compreender como funciona a ferramenta, não necessariamente o parafuso que ela aperta. Como dizem os orientais, não confunda a lua com o dedo que a aponta. Não é porque algo tem sentido pleno quando aplicado aos rigores do cálculo que representa fielmente o mundo lá fora. Tenha cuidado. Estou apenas apontando uma direção, não estou te mostrando o trajeto perfeito.
A modelagem a seguir visa tentar entender como a distribuição da massa explosiva sobre um volume de rocha pode ser simulada. A partir do desenvolvimento apresentado você poderá seguir para a construção de algoritmos de busca, otimização ou mesmo implementar alguns modelos de soft computing para otimizar seu desmonte ou encontrar novas configurações possíveis. Vamos começar olhando de uma maneira diferente para a carga específica.
A carga específica é um dos parâmetros que muitos usam para projetar desmontes. Um termo muito usado como sinônimo, e sintaticamente equivocado, é razão de carga. Sinto causar desapontamento a você que usa o termo razão de carga a muitos anos, mas uma razão para ser chamada como tal, precisa ser calculada em unidades iguais. Por exemplo, maçãs por maças, metro por metro, quilômetros por quilômetros etc. Massa de explosivos por volume de rocha retorna uma unidade de massa por volume, que não é em absoluto uma quantidade adimensional. Veja que a massa de explosivos dividida pela massa de rocha é uma razão! Isto te dá uma chance de se redimir. Para sermos corretos deveríamos utilizar o termo razão de carga apenas quando dividirmos a massa de explosivos pela massa de rocha ou o volume de explosivos pelo volume de rocha. Por estes motivos, mesmo que eles formem um vetor na direção do preciosismo, no texto a seguir utilizaremos a carga específica para designar a unidade \(kg/m^3\) .
Os furos onde colocamos cargas explosivas podem ser modelados como um cilindro. Sem muito medo podemos representar o volume de um furo como
\(v= h \pi r^2 = h \pi \left(\frac{D}{2}\right)^2 = \frac{h \pi D^2}{4}\)
A variável \(h\) é a altura e \(D\) o diâmetro. Utilizarei o diâmetro ao invés do raio para manter a discussão dentro do fraseado comum ao nosso dia a dia. Não te perguntam com que “raio” você vai perfurar, mas com que diâmetro.
A quantidade de explosivos que você coloca dentro do furo tem, grosso modo, duas densidades que podem ser consideras. A primeira é a densidade de massa da substância. Uma grandeza quimicamente definida. É intrínseca à formulação química do explosivo. Aquela que você encontra nos catálogos dos fabricantes. A outra densidade, que é aquela que nos interessa, diz respeito a quanto explosivo você consegue colocar em um furo. Eu chamo esta densidade de densidade de carregamento. Nos encartuchados a densidade de massa e a de carregamento podem apresentar valores muito diferentes. Para emulsão bombeada nem se fala. Aquelas que são gaseificadas quimicamente apresentam uma densidade de massa que é em parte função do confinamento da massa. Partes do fundo do furo serão mais densas que partes próximas ao tampão. Emulsões sensibilizadas com microbalões tendem a sentir menos este efeito. Em NCN’s e similares a densidade de massa e a densidade de carregamento possuem praticamente o mesmo valor. Você pode encontrar a densidade média de carregamento observando quanta massa de explosivo você coloca em um determinado comprimento de furo, observando que a densidade de carregamento (\(\rho)\) é:
\(\rho = \frac{m}{v} = \frac{m}{\frac{h \pi D^2}{4}} = \frac{m}{h}\frac{4}{\pi D^2}\)
O termo \(\frac{m}{h}\) representa em média quanta massa de explosivos você usa para preencher um metro de furo com diâmetro \(D\). É o número que a galera usa para calcular a quantidade de explosivos de um desmonte quando o numero de furos e a quantidade de perfuração é conhecida. Vamos chamá-lo de \(R_l\).
\(\rho = \frac{4 R_l}{\pi D^2} \rightarrow R_l = \frac{\rho \pi D^2}{4}\)
A equação acima vai te ajudar a encontrar a densidade de carregamento que você precisa.
Agora vamos ao volume. A esmagadora maioria usa afastamento x espaçamento x altura. Não vou por esse caminho. Vamos apenas concordar que podemos representar este volume como:
\(V = A H\)
A variável \(A\) representa a área e \(H\) a altura. A área pode ser uma função qualquer. Por enquanto representa área que é destinada a um furo do nosso desmonte. Agora precisamos definir o que entendemos por altura. Veja a figura abaixo.
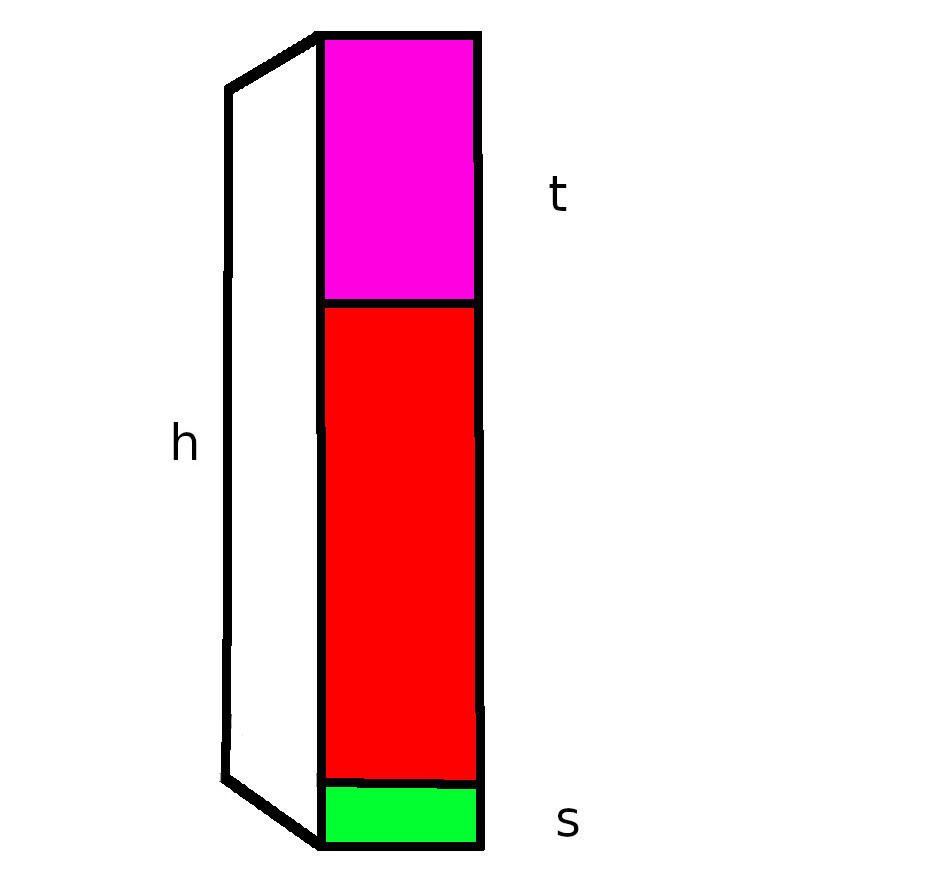
Para a densidade de carregamento, a altura de carga explosiva é \(h-t\). Aqui \(s\) é a sub-furação. Eu ia deixá-la de fora, mas resolvi incluir no modelo para não assustar muito o pessoal ortodoxo. O volume de rocha fica
\(V=A(h-s)\)
A sub-furação é o chorinho de wiskey que você dá para remover o volume.
Agora vamos juntar tudo e formar nossa função carga específica, \(c\):
\(c = \frac{m}{V} = \frac{\rho \pi D^2}{4A}\frac{h-t}{h-s}\,\,\, ;\,\,\, c\rightarrow c(\rho,D,A,h,s,t)\)
Por que fizemos de \(c\) uma função de 6 variáveis? Veja, consideramos \(\rho,D,A,h,s,t\) até agora como independentes, ou seja, podemos escolher quaisquer valores desde que tornem \(c\) válida. Escolher o diâmetro não aletra a escolha ou o valor da área, por exemplo. Depois veremos como vínculos ou restrições alteram nossa função \(c\) e as relações de dependência entre as variáveis, mas por enquanto admita que as seis variáveis são independentes. Fazendo isso, qualquer método de busca ou otimização restringe-se aos valores que as seis variáveis podem assumir. Desta maneira \(c = constante\) representa uma curva de nível para um espaço de 6 dimensões. Não consigo desenhar um gráfico 6D para você visualizar. Você vai precisar invocar a sua capacidade de abstração.
A primeira constatação ao se bater o olho em \(c\) é que se você projetar uma sub-furação com o mesmo comprimento do tampão sua carga específica não se altera. De fato se \(s=t \rightarrow h-s = h-t\) então
\(c =\frac{\rho \pi D^2}{4A}\frac{h-t}{h-s}=\frac{\rho \pi D^2}{4A}(1) = \frac{R_l}{A} = c_0\)
Legal, achamos um ponto notável. A carga específica para uma área por furo \(A\), um diâmetro \(D\) e uma densidade de carregamento do explosivo de \(\rho\), aumenta ou diminui a partir de um valor inicial \(c_0\) dado pela equação acima. Ou, melhor dizendo, \(c\) vai se alterando conforme vamos acrescentando ou removendo sub-furação e/ou tampão.
Queremos saber como a carga específica varia em função de todas as suas variáveis. Imagine que estamos com um volume irregular de rocha para desmontar ou mesmo precisamos simular diversas possibilidades de alturas de bancadas e queremos entender como a distribuição da carga explosiva se altera quando provocamos mudanças nas 6 variáveis da nossa função \(c\).
Uma abordagem possível seria já a queima roupa calcular o gradiente de \(c\) considerando as 6 variáveis independentes:
\(\nabla c = \frac{\partial c}{\partial \rho} \hat{\rho} +
\frac{\partial c}{\partial D} \hat{D} +
\frac{\partial c}{\partial A} \hat{A} +
\frac{\partial c}{\partial h} \hat{h} +
\frac{\partial c}{\partial s} \hat{s} +
\frac{\partial c}{\partial t} \hat{t}\)
Seria muito legal agora se você conseguisse não ter uma interpretação puramente geométrica do vetor gradiente da equação acima.
Vamos calcular termo a termo.
\(\frac{\partial c}{\partial \rho} = \frac{\pi D^2}{4A}\frac{(h-t)}{(h-s)}=\frac{c_0}{\rho}\frac{(h-t)}{(h-s)}\\
\frac{\partial c}{\partial D} = \frac{D \rho \pi}{2A}\frac{(h-t)}{(h-s)}=\frac{2c_0}{D}\frac{(h-t)}{(h-s)}\\
\frac{\partial c}{\partial A} = -\frac{\rho \pi D^2}{4A^2}\frac{(h-t)}{(h-s)}=-\frac{c_0}{A}\frac{(h-t)}{(h-s)}\\
\frac{\partial c}{\partial h} = \frac{\rho \pi D^2}{4A(h-s)}\left(1-\frac{h-t}{h-s}\right)=\frac{c_0}{(h-s)}\left(1-\frac{h-t}{h-s}\right)\\
\frac{\partial c}{\partial s} = \frac{\rho \pi D^2 (h-t)}{4A(h-s)^2}=c_0\frac{h-t}{(h-s)^2}\\
\frac{\partial c}{\partial t} = -\frac{\rho \pi D^2}{4A(h-s)}=-\frac{c_0}{h-s}\)
Juntando tudo
\(\nabla c = \frac{c_0}{\rho}\frac{(h-t)}{(h-s)} \hat{\rho} +
\frac{2c_0}{D}\frac{(h-t)}{(h-s)}\hat{D}
-\frac{c_0}{A}\frac{(h-t)}{(h-s)}\hat{A}
+\frac{c_0}{(h-s)}\left(1-\frac{h-t}{h-s}\right)\hat{h}
+c_0\frac{h-t}{(h-s)^2}\hat{s}
-\frac{c_0}{h-s}\hat{t}
\)
Ainda, podemos simplificar e obter:
\(\nabla c = c_0\frac{(h-t)}{(h-s)}\left[\frac{1}{\rho}\hat{\rho} + \frac{2}{D}\hat{D} -\frac{1}{A}\hat{A} + \frac{1}{(h-t)}\left(1 – \frac{h-t}{h-s}\right)\hat{h} + \frac{1}{(h-s)}\hat{s} -\frac{1}{(h-t)}\hat{t}\right]\)
Olhe a ultima equação e lembre-se da definição de gradiente. Fica muito claro, a partir de uma carga específica definida em um ponto \((\rho_0,D_0,A_0,h_0,s_0,t_0)\) o vetor \(\nabla c\) mostra a “direção” em que a carga específica sofre a máxima variação. Duas observações aqui. Coloquei versores para indicar quem é quem no vetor. O objetivo é facilitar o entendimento para quem está um pouco enferrujado no cálculo, achei melhor do que colocar coordenadas do tipo \(e_0,e_1…e_n\).
Por direção não entenda algo como um caminho no sentido de trajetória em um mundo 3D. Talvez o conceito de direção fique mais claro com o exemplo a seguir.
Seu desmonte contempla uma altura de \(13,5m\) com furos de diâmetro \(3”\). Suponha que todas as suas variáveis assumam estes valores:
\(\rho = 1000kg/m^3
\\
A = 7m^2
\\
D = 3”= 0,076m
\\
h = 13m
\\
t = 1,5m
\\
s = 0,5m\)
O calculo de \(c_0\) retorna \(c\approx0,6481 kg/m^3\) e o gradiente, \(\nabla c\), neste ponto é:
\(\nabla c = 0,6481\frac{13-1,5}{13-0,5}\left[\frac{1}{1000}\hat{\rho} + \frac{2}{0,076}\hat{D}-\frac{1}{7}\hat{A}+\frac{1}{(13-1,5)}\left(1 – \frac{13-1,5}{13-0,5}\right)\hat{h}+\frac{1}{(13-0,5)}\hat{s} -\frac{1}{(13-1,5)}\hat{t}\right]
\\
\nabla c = 0,000596\hat{\rho} + 15,690\hat{D} – 0,085174\hat{A} + 0,0041476\hat{h} + 0,047698\hat{s}-0,051845\hat{t}\)
Aproveitamos o embalo e calculamos o módulo \(|\nabla c|\)
\(|\nabla c| = \sqrt{(0,000596)^2 + (15,690)^2 + (-0,085174)^2 + (0,0041476)^2 + (0,047698)^2 +(-0,051845)^2}
\\
|\nabla c| \approx 15,690kg/m^3\)
Vamos interpretar fisicamente estes números. O vetor gradiente diz que se você estiver nesta configuração de desmonte, você vai produzir mais variação da carga específica se alterar o diâmetro do que qualquer outra variável. Veja que o “peso” do diâmetro no vetor é muito maior que o das outras variáveis. Se você aumentar a componente da área por furo (malha) ou o tampão você vai diminuir \(c\) e vice-versa. Observe que a contribuição da densidade do explosivo é muito menor que a do diâmetro. Isto significa que para aumentar ou diminuir \(c\) é muito mais eficiente alterar o diâmetro do que a densidade do explosivo.
Os componentes de \(\nabla c\) nos mostram que o diâmetro do furo produz variações de \(c\) em uma escala muito maior do que as outras variáveis. Se queremos mudanças bruscas, brincamos com \(D\). Se é necessário um ajuste fino deixamos \(D\) quietinho e vamos alterando as outras variáveis.
O módulo do gradiente te diz qual será a maior taxa de variação possível para nossa função \(c\). Qualquer “sentido” que tomarmos, por exemplo, somente na direção da altura e tampão, a taxa de variação da carga específica será menor que o módulo do gradiente.
Você pode utilizar o conceito de derivada direcional para montar sistemas baseados nas equações do gradiente. Por exemplo, para quais valores de tampão e altura de perfuração \(c\) varia a uma taxa constante? Essa pergunta é matematizada com a ajuda de um vetor
\(\vec{v} = x\hat{h} + y\hat{t}\)
Em que \(x\) representa a alteração de altura e \(y\) a alteração de tampão. Fazendo
\(\nabla_{\vec{v}} c = \nabla c \cdot \frac{\vec{v}}{|\vec{v}|}\)
projetamos as componentes necessárias do gradiente sobre a o vetor \(\vec{v}\).
Em textos futuros vou te mostrar como escrever algoritmos para buscas e otimizações utilizando computação evolutiva e algumas meta heurísticas aplicadas no domínio de \(c\).
Como uma pequena demonstração, vejamos um exemplo simples de como extrair informações correlacionadas a carga específica, deixando a abordagem computacional para outra ocasião.
Vamos considerar que \(s\) não pode ser livremente escolhida. Não podemos fazer a sub-furação infinitamente grande. Não faz sentido. Sua eficácia vai até um limite. Não adianta perfurar a mais indefinidamente achando que isso vai te ajudar. Chegará um ponto em que qualquer incremento de carga não terá efeito sobre a cota de corte que você quer. Para nosso caso, diremos que \(s\) depende da área do furo, \(s\rightarrow s(A)\).
Também faremos o tampão uma função da altura de corte, assim \(t\rightarrow t(h)\). O por quê disso já vai ficar claro.
Com estas modificações \(c\) fica:
\(c =\frac{\rho \pi D^2}{4A}\frac{h-t(h)}{h-s(A)}\)
Agora, vejamos como \(c\) se altera quando brincamos com a altura \(h\)
\(\frac{\partial c}{\partial h} = \frac{\rho \pi D^2}{4A}\frac{d}{dh}\frac{h-t(h)}{h-s}
\\
\frac{\partial c}{\partial h}=\frac{\rho \pi D^2}{4A}\left( \frac{(1-\frac{d}{dh}t(h))(h-s) – (h-t(h))} {(h-s)^2}\right)
\\
\frac{\partial c}{\partial h}=\frac{\rho \pi D^2}{4A(h-s)^2}\left( (1-\frac{d}{dh}t(h))(h-s) – (h-t(h))\right)
\\
\frac{\partial c}{\partial h}\frac{4A(h-s)^2}{\rho \pi D^2}=\left( (1-\frac{d}{dh}t(h))(h-s) – (h-t(h))\right)
\\
\frac{\partial c}{\partial h}\frac{4A(h-s)^2}{\rho \pi D^2}= h-s-\frac{d}{dh}t(h)(h-s) – h+t(h)
\\
\frac{\partial c}{\partial h}\frac{4A(h-s)^2}{\rho \pi D^2}= -s-\frac{d}{dh}t(h)(h-s) + t(h)
\\
\frac{\partial c}{\partial h}\frac{4A(h-s)^2}{\rho \pi D^2} + s= -\frac{d}{dh}t(h)(h-s) + t(h)
\\
\frac{\partial c}{\partial h}\frac{4A(h-s)^2}{\rho \pi D^2 (h-s)} + \frac{s}{(h-s)}= -\frac{d}{dh}t(h) + \frac{t(h)}{(h-s)}
\\
\frac{\partial c}{\partial h}\frac{4A(h-s)}{\rho \pi D^2} + \frac{s}{(h-s)}= -\frac{d}{dh}t(h) + \frac{t(h)}{(h-s)}
\\
\frac{d}{dh}t(h) – \frac{t(h)}{(h-s)} = -\frac{\partial c}{\partial h}\frac{4A(h-s)}{\rho \pi D^2} – \frac{s}{(h-s)}\)
Como \(s\) depende somente de \(A\) tratamos ela como constante quando diferenciando em relação a \(h\). Fiz o algebrismo da maneira mais didática possível. Aqui não temos preocupação com número de páginas.
Se não queremos que \(c\) varie com o tampão e com qualquer outra variável, então
\(\frac{d}{dh}t(h) = 0
\\
\frac{\partial c}{\partial h} = 0\)
e a equação diferencial que deduzimos se torna
\(-\frac{t(h)}{(h-s)} = – \frac{s}{(h-s)}
\\
t(h) = s\)
Chegamos a mesma conclusão que antes. Faça o tampão igual a sub-furação que \(c\) não vai variar.
Mas fazer \(t(h) = s\) não é a única maneira de fazer \(c\) constante quando se varia a altura. Podemos nos perguntar se existem valores de \(t\) que mantêm \(c\) inalterada conforme a altura varia. Ou, em equivalente linguagem matemática:
\(\frac{d}{dh}t(h) – \frac{t(h)}{(h-s)} = -0\frac{4A(h-s)}{\rho \pi D^2} – \frac{s}{(h-s)}
\\
\frac{d}{dh}t(h) – \frac{t(h)}{(h-s)} + \frac{s}{(h-s)} = 0\)
Resolvendo esta última ED podemos encontrar os valores de \(t\) que quando aplicado em função da altura mantem a carga específica constante.
Lembre lá de calculo 3 que você aprendeu um negócio chamado fator integrante. Não vou abrir um parenteses para explicar, mas pode conferir aqui. Calculando o fator interante
\(FI = e^{-\int\frac{1}{(h-s)}} = \frac{1}{(h-s)}\)
odemos transformar nossa ED em uma equação separável multiplicando o FI em ambos os lados:
\(\frac{d}{dh}t(h)\frac{1}{(h-s)} – \frac{t(h)}{(h-s)}\frac{1}{(h-s)}= – \frac{s}{(h-s)}\frac{1}{(h-s)}
\\
\frac{d}{dh}t(h)\frac{1}{(h-s)} – \frac{t(h)}{(h-s)^2}= – \frac{s}{(h-s)^2}
\\
\frac{d}{dh}\frac{t(h)}{h-s} = – \frac{s}{(h-s)^2}\)
Agora ficou fácil, veja:
\(\frac{d}{dh}\frac{t(h)}{h-s} = – \frac{s}{(h-s)^2}
\\
\frac{t(h)}{h-s} = – \int \frac{s}{(h-s)^2}dh
\\
\frac{t(h)}{h-s} = \frac{s}{h-s} +Cte
\\
t(h) = s + Cte(h-s)\)
Lembrando que partimos de uma configuração inicial, como no nosso \(c_0\), aqui também temos um tampão inicial associado a uma altura inicial, \((t_0;h_0)\).
\(t_0 = s + Cte(h_0-s) \rightarrow Cte = \frac{t_0-s}{h_0-s}
\\
t(h) = s + (t_0-s)\frac{(h-s)}{h_0-s}\)
Essa equação acima, que representa uma reta, diz que se você calcular o tampão por ela \(c\) vai permanecer constante. Vamos verificar.
Começamos com uma configuração assim:
\(\rho = 1000kg/m^3
\\
A = 7m^2
\\
D = 3”= 0,076m
\\
h_0 = 10m
\\
t_0 = 1,5m
\\
s = 0,5m\)
E fazendo o tampão obedecer \(t(h) = s + (t_0-s)\frac{(h-s)}{h_0-s}\) obtemos a tabelinha abaixo
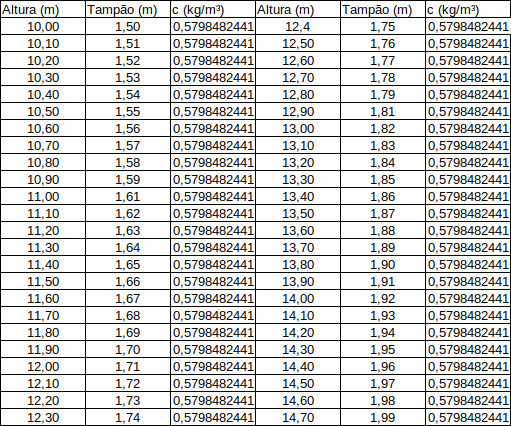
Obviamente, seguir a regra de tampão obtida pode não ter muito sentido na prática. Se a inclinação da reta da equação do tampão for muito acentuada, pequenas variações na altura de corte produzirão grandes variações na
altura do tampão e mesmo que a carga específica permaneça constante, isto pode afetar significativamente a qualidade do desmonte.
Perceba que você pode substituir a equação do tampão na definição de \(c\):
\(c = \frac{\rho \pi D^2}{4A}\frac{h-t}{h-s}
\\
c = \frac{\rho \pi D^2}{4A}\frac{h-(s + (t_0-s)\frac{(h-s)}{h_0-s})}{h-s}
\\
c = \frac{\rho \pi D^2}{4A}\left(1-\frac{(t_0 -s)}{(h_0-s)}\right)\)
Repare que \(c\) não depende da altura, vai ser sempre constante. Dê uma olhadinha nas componentes do tampão e a da altura lá do gradiente que definimos acima. Se juntamos as duas obtemos:
\(\frac{\partial c}{\partial h} =-\frac{\partial c}{\partial t}\left(1-\frac{h-t}{h-s}\right)\)
Dentre outras coisas, perceba que se não existe variação da carga específica com o tampão, não existe também variação da carga específica com a altura. E vice-versa. A mesma informação que encontramos a pouco quando fizemos \(c\) não depender da altura fazendo com que o tampão ficasse sobre o imagem da reta \(t(h)\). Seria muito legal se você observasse as informações que podemos retirar dos inúmeros sistemas que podemos montar com a abordagem que estou te mostrando. Eu poderia abrir muito mais o leque aqui, mas ficaria um texto muito longo. Vamos devagar.
Para fechar, vou te mostrar duas coisas: como de certa forma você consegue controlar a variação de \(c\) fazendo com que \(t(h)\) assuma a forma de outras funções. E por último, como incluir um modelo simples de previsão de flyrock nisso tudo.
Veja, encontrar a solução geral de
\(\frac{d}{dh}t(h) – \frac{t(h)}{(h-s)} = -\frac{\partial c}{\partial h}\frac{4A(h-s)}{\rho \pi D^2} – \frac{s}{(h-s)}\)
envolve, necessariamente, conhecer como a carga específica varia com a altura de corte. O termo \(\frac{\partial c}{\partial h}\) diz isso de forma gritante pra nós.
Mas veja, admitimos que \(\frac{\partial c}{\partial h}\) possui uma representação analítica. Isso quer dizer que:
\(\frac{\partial c}{\partial h}\equiv f_r(h)\)
A implicação disso é que pode existir uma função, digamos, \(\eta(h)\) tal que:
\(\eta(h)=\int f_r(h)dh + Cte\)
Fazendo a substituição:
\(\frac{d}{dh}t(h) – \frac{t(h)}{(h-s)} = -f_r(h)\frac{4A(h-s)}{\rho \pi D^2} – \frac{s}{(h-s)}\)
Uma solução para a ED acima através do uso do mesmo fator integrante que calculamos antes seria:
\(\frac{d}{dh}\left(\frac{t(h)}{(h-s)}\right)= -\frac{f(h)4A} {\rho\pi D^2} – \frac{s}{(h-s)^2}
\\
\frac{t(h)}{(h-s)} =-\frac{4A} {\rho\pi D^2}\int f(h)dh + -s\int\frac{1}{(h-s)^2}dh
\\
t(h) = \frac{-4A(h-s)}{\rho \pi D^2} \eta(h) + s + K(h-s)\)
Perceba como incluímos \(\eta(h)\) na solução acima pelo uso de \(\eta(h)=\int f_r(h)dh + Cte\).
A solução geral encontrada é particularizada sob a luz de uma das condições adotadas até agora: para uma \(h_0\) temos um \(t_0\) associado, de forma que a constante \(K\) que aparece na equação é:
\(t_0 = \frac{-4A(h_0-s)}{\rho \pi D^2} \eta(h_0) + s + K(h_0-s)
\\
K = \frac{(t_0-s)}{(h_0-s)}+ \frac{4A\eta(h_0)}{\rho \pi D^2}\)
Substituindo na solução geral encontramos a solução particular:
\(t(h) = \frac{4A(h-s)}{\rho \pi D^2}(\eta(h_0) – \eta(h)) + \frac{(t_0-s)}{(h_0-s)}(h-s) + s\)
Esta função \(t(h)\) diz como deve ser a altura do tampão se você que que a carga específica obedeça a regra \(\eta(h)\). Vamos substituir nosso novo \(t(h)\) na definição \(c\).
\(c =\frac{\rho \pi D^2}{4A(h-s)}(h-t(h))
\\
c =\frac{\rho \pi D^2}{4A(h-s)}(h-\left(\frac{4A(h-s)}{\rho \pi D^2}(\eta(h_0) – \eta(h)) + \frac{(t_0-s)}{(h_0-s)} + s\right))
\\
c = \frac{\rho \pi D^2}{4A}\left(1-\frac{(t_0-s)}{(h_0-s)}\right)-(\eta(h_0) – \eta(h))\)
Observe que a taxa de variação da carga específica em relação a altura de corte é dada somente pela função \(\eta(h)\). De fato, se derivamos \(c\) em relação a altura de corte obtemos:
\(\frac{\partial}{\partial h}c=\frac{d}{dh}\left[\frac{\rho \pi D^2}{4A}\left(1-\frac{(t_0-s)}{(h_0-s)}\right)-(\eta(h_0) – \eta(h))\right]
\\
\frac{\partial}{\partial h}c = 0 – 0 – 0 + \frac{d}{dh}\eta(h)
\\
\frac{\partial}{\partial h}c = \frac{d}{dh}\eta(h)\)
Ou seja, a taxa de variação da carga específica em função da altura de corte em rocha é controlada apenas pela escolha da função \(\eta(h)\).
Estabelecendo um valor para \(\frac{\partial}{\partial h}c\) podemos obter uma regra (ou função) associada aos valores de tampão que devemos utilizar para manter a variação da carga específica dentro do planejado por \(\eta(h)\). Por exemplo, se por algum motivo qualquer desejamos que quanto maior a altura de corte mais carga explosiva queremos, isto implica que:
\(f_r(h)=\delta\)
Sendo \(\delta$\) a taxa constante com que a carga específica varia com a altura e corte. Portanto, \(\delta\) tem unidade \(kg.m^{-3}/m\).
Integrando em relação a \(h\) obtemos:
\(\eta(h)=\int \delta dh
\\
\eta(h)=\delta h + Cte\)
Substituindo o resultado
\(c = \frac{\rho \pi D^2}{4A}\left(1-\frac{(t_0-s)}{(h_0-s)}\right)-(\eta(h_0) – \eta(h))
\\
c = \frac{\rho \pi D^2}{4A}\left(1-\frac{(t_0-s)}{(h_0-s)}\right)-\delta h_0 – Cte + \delta h + Cte
\\
c = \frac{\rho \pi D^2}{4A}\left(1-\frac{(t_0-s)}{(h_0-s)}\right)+ \delta(h – h_0)
\\
\\
t(h) = \frac{4A(h-s)}{\rho \pi D^2}(\eta(h_0) – \eta(h)) + \frac{(t_0-s)}{(h_0-s)}(h-s) + s
\\
t(h) = -\frac{4A(h-s)}{\rho \pi D^2}\delta(h – h_0) + \frac{(t_0-s)}{(h_0-s)}(h-s) + s\)
Estas duas funções dizem que se você seguir o tampão dado pela regra \(t(h)\) sua carga específica vai crescer linearmente a uma taxa \(\delta\). Veja no próximo gráfico os valores do tampão em função da altura mapeados para a carga específica para os seguintes valores iniciais
\(\rho = 1000kg/m^3
\\
A = 7m^2
\\
D = 3”= 0,076m
\\
h_0 = 10m
\\
t_0 = 1,5m
\\
s = 0,5m\)
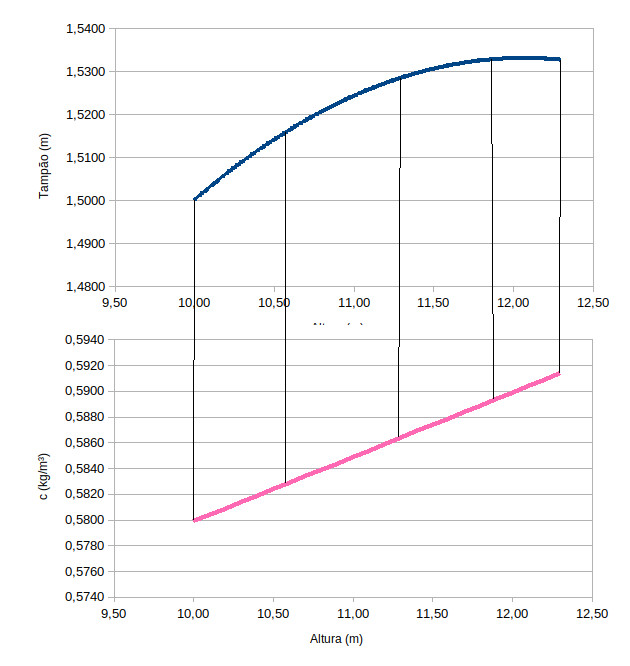
Os dados que foram usados para gerar os gráficos acima foram:
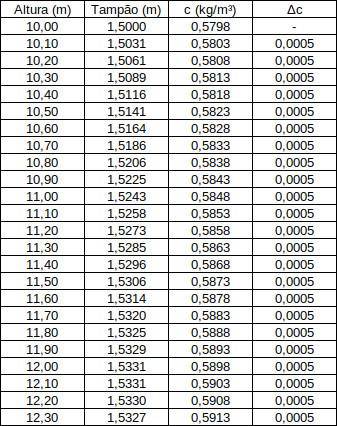
Veja que a variação da carga específica (\(\Delta c\)) é constante e igual àquela que estipulamos.
A princípio, qualquer escolha de \(\eta(h)\) que gere um sistema físico plausível pode ser usada para modelar ou simular diversas configurações de geometria de malha e configurações de carga explosiva.
A função \(\eta(h)\) não é uma entidade real; a carga específica é simplesmente a quantidade de explosivos que se utiliza para desmontar uma certa quantidade de rocha e \(\eta(h)\) não é necessária para isso. Porém, \(\eta(h)\) pode nos mostrar que regra devemos seguir quanto a altura do tampão para que nossa carga específica varie desta ou daquela maneira, dependendo das considerações que estipularmos. Qual é a regra que \(\eta(h)\) estabelece e se esta regra é fisicamente possível de ser implementada ou mesmo se é economicamente viável, cabe ao projetista do desmonte decidir.
Eu não coloquei as medidas geométricas de afastamento e espaçamento até agora porque, sinceramente, acho parâmetros muito simplistas, além de conduzirem a um erro grosseiro no calculo de volume que não entendo até hoje por que ainda são utilizados. Mas se você esta angustiado com isso vou quebrar seu galho.
Para introduzir os seus queridinhos afastamento (B) e espaçamento (E) vamos utilizar também a relação entre eles.
\(\beta = \frac{E}{B}\)
A famosa relação \(\beta\) que é palco de discussões acaloradas sobre qual valor dentro do intervalo dos numeros reais [1 ;2] produz o melhor resultado. Meu conselho é: não caia nessa. Reduzir a complexidade de um possível ponto ótimo e universal do desmonte de rocha a uma relação entre \(B\) e \(E\) é muito simplista. Eu poderia até arriscar e dizer que é um bode na sala para desviar a atenção da nossa completa ignorância sobre os fundamentos da teoria do desmonte. Algo como “é o que tem pra hoje”.
Se te faz feliz, podemos inserir \(B\) e \(E\) desta maneira
\(A = (B)(E)
\\
\beta B = E
\\
A = B^2\beta
\\
c = \frac{\rho \pi D^2}{4 B^2\beta}\left(1-\frac{(t_0-s)}{(h_0-s)}\right)+ \delta(h – h_0)\)
Ou, se você quer partir do início:
\(c = \frac{\rho \pi D^2}{4B^2\beta}\frac{h-t}{h-s}
\\
\left(\frac{B}{D}\right)^2 = \frac{\rho \pi}{4c\beta}\frac{h-t}{h-s}\)
Pode usar estes dois modelos para brincar de encontrar “malhas”. Só preste atenção nas limitações que o uso de \(B\) e \(E\) carregam.
Por ultimo, vou te mostrar um pequeno exemplo de como incluir o modelo de flyrock de McKenzie. Este modelo está no Blasters Handbook e é derivado de um paper de McKenzie se não me engano publicado em 2009. Se quer os detalhes pesquise na base de dados da ISEE, vais encontrar com certeza. O paper se chama Flyrock Range and Fragment Size Prediction.
Não cabe aqui julgar se é o melhor modelo de previsão de flyrock ou não. É apenas um exemplo de como incorporar informações externas. Você é altamente encorajado a usar seus modelos e deduções.
Começamos admitindo a hipótese que queremos uma carga específica constante, mas temos alturas de corte variáveis.
Observando a reta:
\(t(h) = s + (t_0-s)\frac{(h-s)}{h_0-s}\)
Vamos escolher um valor inicial \(t_0\) com base na profundidade de carga escalonada – SDB (do inglês Scaled Depth of Burial)
\(SDB = \frac{t+\frac{1}{2}MD}{Q^{\frac{1}{3}}}\)
As variáveis são:
t = tampão.
M = fator de contribuição de aproximação de carga esférica.
D = diâmetro do furo.
Q = carga explosiva associada à aproximação de carga esférica.
O fator \(M\) admite um valor máximo de 8 para diâmetros \(d<100mm\) e um valor máximo de 10 para \(d\geq100mm\) (McKenzie, 2009). Ou, dito de outra maneira, para diâmetros menores que 100mm considere um comprimento de carga explosiva de \(8D\), para diâmetros maiores, \(10D\).
Definido \(M\), o valor da carga correspondente \(Q\) pode ser obtido através da densidade de massa efetiva do explosivo \(\rho\):
\(\rho = \frac{Q}{V}
\\
\rho = \frac{4Q}{\pi\,D^2\, MD}
\\
\rho = \frac{4Q}{\pi\,D^3\,M}
\\
Q = \frac{\rho\,\pi\,D^3\,M}{4}\)
Substituindo na SDB:
\(SDB = \frac{t+\frac{1}{2}MD}{\biggl(\frac{\rho\,\pi\,D^3\,M}{4}\biggr)^{\frac{1}{3}}}\)
Se \(t_0\) está, de certa forma, condicionado a um valor de SDB, digamos \(SDB_{t0}\), podemos rearranjar os termos e obter:
\(t_0 = D\Biggl[SDB_{t0} \Biggl(\frac{\rho\,\pi\,M} {4}\Biggr)^{\frac{1}{3}} -\frac{1}{2}M \Biggr]\)
Definir um valor fixo para a SDB implica, inevitavelmente, em utilizar o mesmo valor do tampão para todos os furos, independente da altura de corte em rocha. Para superar isso, podemos definir uma faixa de valores de SDB, como para \(t_0\) uma \(SDB_{t0}\) e para um valor de \(t_{n}\) uma \(SDB_{t_{n}}\). Teremos então duas equações:
\(t_0 = D\Biggl[SDB_{t0} \Biggl(\frac{\rho\,\pi\,M} {4}\Biggr)^{\frac{1}{3}} -\frac{1}{2}M \Biggr]
\\
t_{n} = D\Biggl[SDB_{t_{n}} \Biggl(\frac{\rho\,\pi\,M} {4}\Biggr)^{\frac{1}{3}} -\frac{1}{2}M \Biggr]\)
Se a carga específica deve ser constante escrevemos:
\(t(h) = s + (t_0-s)\frac{(h-s)}{h_0-s}
\\
t_{n} = s + (t_0-s)\frac{(h-s)}{h_0-s}
\\
h = \frac{(t_n-s)}{(t_0-s)}(h_0-s) + s = h_{max}\)
A equação acima mostra a altura máxima que impomos ao nosso modelo. Ou seja, o tampão inicial \(t_0\), associado a \(SDB_{t0}\), está associado à altura inicial de corte em rocha \(h_0\). O tampão \(t_{n}\) está associado a \(SDB_{t_{n}}\) e conduz a maior altura de corte possível, \(h_{max}\), partindo de \(h_0\). Esta altura máxima conduz a \(SDB_{t_{n}}\).
Para fixar, um pequeno tutorial.
1 – Para a menor altura encontre um tampão baseado na SDB. Assim você define \(t_0\), \(h_0\) e \(SDB_{t_0}\).
2 – Encontre um valor de \(t_n\) que gere um valor aceitável para SDB. Assim você garante que os furos vão apresentar SDB dentro do limite \([SDB_{t_0};SDB_{t_n}]\) que você definiu.
3 – Encontre a altura máxima possível para que o modelo seja válido.
4 – O tampão para o intervalo de alturas \([h_0;h_{max}]\) é dado por
\(t(h) = s + (t_0-s)\frac{(h-s)}{h_0-s}\)
Pronto, neste modelo matemático você gera tampões que estão dentro de um limite seguro e uma carga específica constante independente da altura de corte em rocha, desde que a altura esteja dentro de um intervalo \([h_0;h_{max}]\).
A partir destas deduções você pode montar uma enorme quantidade de modelos para simular algum assunto em particular. Eu apresentei apenas alguns, muito básicos na verdade, mas é um ponto de partida.
Os modelos que descrevi são na melhor das hipóteses um pequeno guia para simulação. Não absorvem toda a complexidade do fenômeno desmonte de rochas. É apenas uma maneira de tentar entender como mudanças que fazemos na malha de perfuração, diâmetro e nas outras variáveis associadas podem influenciar na distribuição da massa explosiva pelo volume de rocha, mesmo este volume sendo um sólido irregular.
Espero que você tenha aproveitado. Segue o seu caminho, tenta simular, melhorar o que aqui foi apresentado e se você encontrar algo legal, me avisa. Os vídeos a seguir mostram alguns desmontes onde eu utilizei metodologias parecidas para a modelagem de cargas, malhas, temporização e análise de flyrock. A grande diferença é que nestes desmontes eu tratei as variáveis como distribuições de probabilidades. Outra hora a gente conversa sobre isso.
Valeu
