Não se pode negar, quase todo mundo da área ignora os efeitos das dispersões dos acessórios não-elétricos. Em alguns casos estas variações no tempo de retardo não chegam a ser um problema. Mas em situações, digamos, mais delicadas, ignorar a dispersão não é muito saudável.
Todos, todos os acessórios não-elétricos de qualquer fabricante do mundo possuem dispersões no tempo de retardo. Não é culpa dos fabricantes, é simplesmente um dos limites da tecnologia, não tem como evitar. Existem acessórios mais precisos / acurados, mas a dispersão ainda está lá, presente sorrateiramente no misto pirotécnico, pronta par te pegar de surpresa…
Se você perguntar para o seu fornecedor de explosivos favorito sobre dispersão, ele não vai negar que tenha, mas provavelmente a resposta será algo como “não passa de 5%" ou "7%” ou qualquer valor percentual. Não é mentira, geralmente os valores estão próximos a estes, mas o que realmente importa é a distribuição associada, não o seu intervalo. A dispersão interfere no sequenciamento, controle de vibrações e também em conceitos como a regra dos 8ms e a carga máxima por espera.
A taxa percentual de dispersão não é constante, e nem pode. A dispersão deriva da incerteza sobre o tempo de queima do misto. É impossível produzir um misto exatamente igual ao outro e lotes diferentes com o mesmo tempo de queima. Quanto maior é o tempo de retardo, mais incerteza vem associada ao não-elétrico. Perceba que os tempos de retardo entre não-elétricos em sequência vai aumentando conforme o tempo absoluto de retardo aumenta. Dificilmente um fabricante que consegue produzir, digamos, uma peça com 1500ms e outra com 1520ms. Ele pode até fabricar, mas não te dará garantia que vai funcionar como você imagina.
A porcentagem de dispersão é função do tempo de retardo, quanto maior o tempo, maior a incerteza. Mas isso não é o mais importante, o importante é como está distribuída a variação no tempo.
Por exemplo, se a única informação sobre um retardo é que a taxa percentual de dispersão é \(d\) então o tempo de retardo provável, \(t_r\), é de:
\(t_r = t_m \pm \frac{d}{2}t_m\)
Em que \(t_m\) é o tempo médio. Se cada \(t_r\) tem probabilidade igual de ocorrência, isto é, qualquer valor dentro do intervalo
\([t_m(1-\frac{d}{2});t_m(1+\frac{d}{2})]\)
tem a mesma chance de ser contemplado, então a distribuição dos tempos é uniforme. Neste caso, não existe um valor privilegiado. Veja na figura abaixo a distribuição associada ao valores inteiros do intervalo \([20;30]\). Qualquer valor, no limite, tem probabilidade de \(1/11 \approx 9,1\%\) de ocorrer.
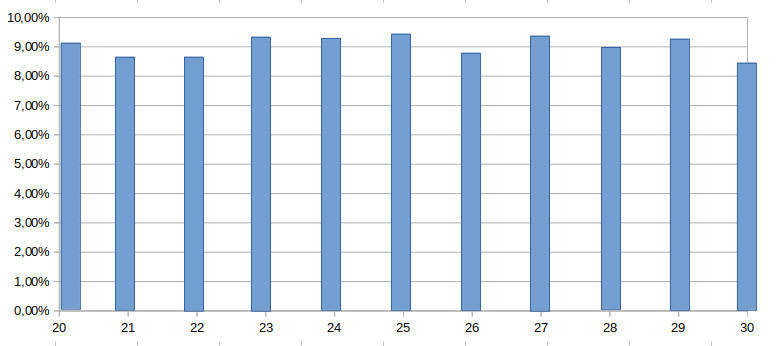
Mas este tipo de distribuição não ocorre no nosso caso, não consegue representar (felizmente!) a densidade de probabilidade dos tempos de retardo. Geralmente uma distribuição normal é associada à dispersão. Para cravar de forma contundente a aderência dos dados à uma distribuição normal seria necessária uma análise um pouco mais rigorosa. Alguns dados que possuo, que consegui a muito tempo atrás, se comportam muito bem quando são solicitados a serem normais. Deste modo, vamos tratar a dispersão assim, como distribuições normais, afinal o enfoque matemático que será dado pode ser facilmente alterado para englobar outras distribuições.
Quando dizemos que a distribuição é normal, queremos dizer que o tempo de retardo se espalha da maneira mostrada na figura abaixo.
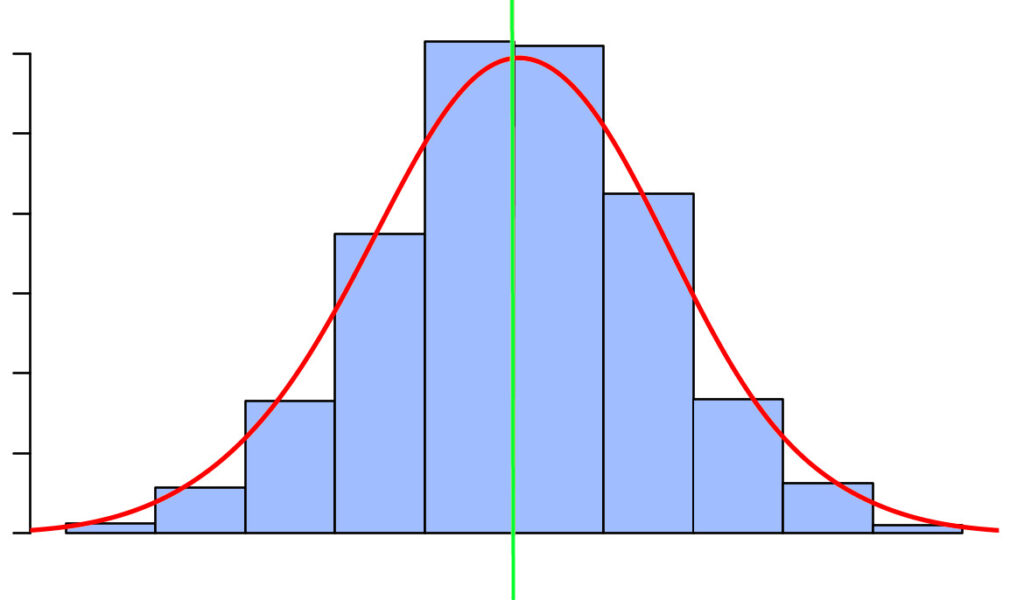
A linha vermelha representa dados contínuos; as barras azuis verticais são dados discretos.
Admitindo a normalidade, podemos representar os tempos de retardos por uma média e por um desvio padrão.
\(t_r=N(t_m,\sigma_r)\)
Por exemplo, suponha um retardo de 25ms com \(t_m = 24,676ms; \sigma = 2,75ms\) (acredite, isto são valores comuns para um bom retardo de 25ms), podemos simular a detonação virtual de, digamos, 10 milhões de peças deste retardo com o pequeno programa em C. O programa da lista abaixo gera 10 milhões de números normalmente distribuídos, com média \(t_m = 24,676ms\) e desvio padrão \(\sigma = 2,75ms\) e produz um histograma contendo todos os valores inteiros encontrados, isto é, o programa trunca os valores. Por exemplo, um valor de 26,9787ms será truncado para 26ms e assim por diante.
#include <stdio.h>
#include <math.h>
// funçoes de dsitribuição de probabilidade
#include <gsl/gsl_cdf.h>
// geração de números aleatórios
#include <gsl/gsl_rng.h>
#define MAX_ARRAY 100
#define SIMULACOES 10000000
// cada indice deste array representa um tempo de retardo. // Indice 10 -> 10ms ...
int delays[MAX_ARRAY];
int main (int argc, char ** argv)
{
// setup do ambiente da gsl
const gsl_rng_type *T;
gsl_rng *r;
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc(T);
// media e desvio padrão
const double media = 24.676;
const double sd = 2.75;
// inicialização do array
for(int i = 0; i < MAX_ARRAY; i++)
{
delays[i] = 0;
}
//iteracao das simulacoes
for(int i = 0; i < SIMULACOES; i++)
{
// numero aleatório entre 0.000 e 1.000
double u = gsl_rng_uniform(r);
/* Retorna um numero dentro de uma distribuição normal
padrão N(0,1)
*/
double x = gsl_cdf_ugaussian_Pinv(u);
/* gsl_cdf_ugaussian_Pinv retorna um Z-score, então
mapeamos o valor de Z para nossa distribuição
*/
x = x * sd + media;
// aqui guardamos somente a parte inteira (truncamos)
int indice = trunc(x);
if(indice < MAX_ARRAY)
delays[indice] = delays[indice] + 1;
}
// Imprimimos os valores na saída padrão
for(int i = 0; i < MAX_ARRAY; i++)
{
// se existe um valor (C trata valores 0 como false)
if(delays[i])
{
double porc = ((double)delays[i] / SIMULACOES) * 100.00;
printf("%dms : %d :==> %.5f%%\n", i, delays[i], porc);
}
}
// liberando a memória alocada por gsl_rng_alloc
gsl_rng_free(r);
return 0;
}O código acima utiliza a biblioteca GSL – GNU Scientific Library. Dá para melhorar muito o programinha acima. Mas aqui o foco é outo. Eu salvei o arquivo fonte como MC25ms.c e compilei no Ubuntu 20.04 com
gcc -o MC25 -Wall MC25ms.c -lgsl -lm -lgslcblas
A saída do programa esta na figura abaixo.
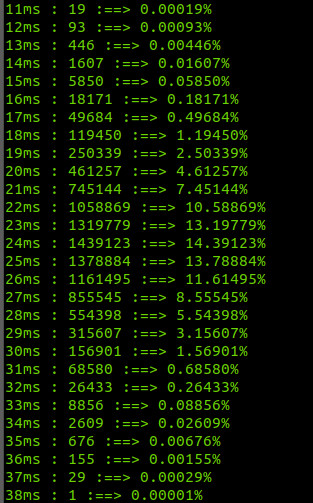
Este histograma não que dizer que a probabilidade do retardo detonar com 25ms é 13,78%, mas que 13,78% é a chance dele ser encaixado no tempo 25ms, que vai de 25.0000 a 25.9999999…
Vamos comparar nossa pequena simulação Monte Carlo com a integração da Função Densidade de Probabilidade – FDP (adoro essa abreviação) sobre um intervalo. A FDP da normal é:
\(f_X(x) = \frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ – \frac{1}{2}\big(\frac{{x – \mu}}{\sigma}\big)^2} \quad -\infty< x < \infty\)
Se integramos a função acima sobre um intervalo qualquer \([a;b]\), obtemos a probabilidade de que \(X\) esteja dentro do intervalo.
\(P(a < X < b) = \int\limits_a^b {{\frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ – \frac{1}{2}\big(\frac{{x – \mu}}{\sigma}\big)^2}}}dx\)
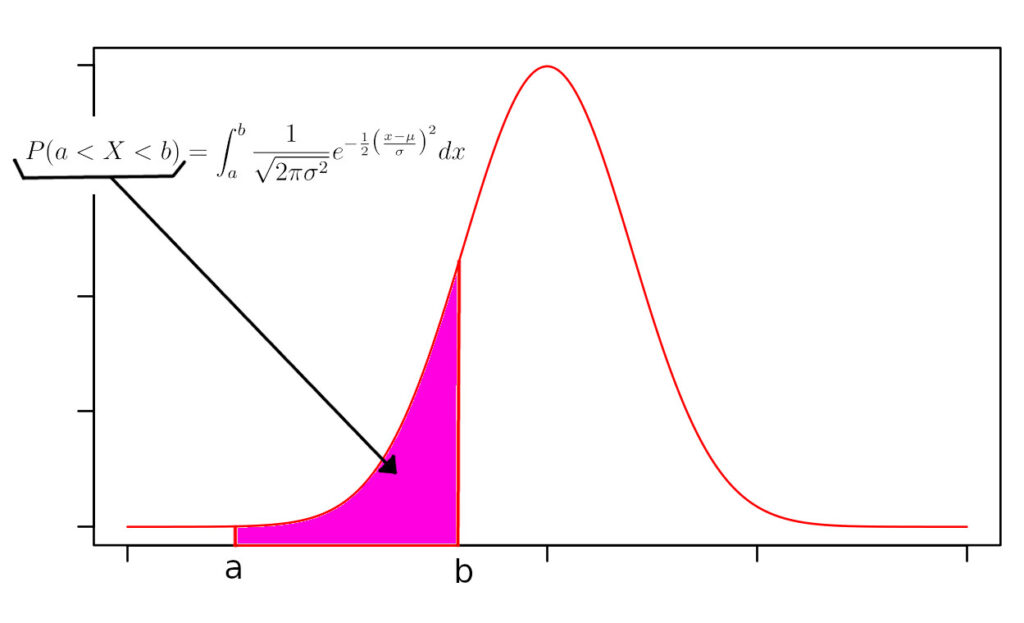
Todos que tentaram encontrar uma solução analítica para a integral acima falharam. Conjectura-se que nem existe. Por isso o pessoal agrupa os valores da integral na famosa tabela de z-score. Mas os nerds costumam colocar os limites de integração como \((-\infty;b)\). Veja a figura abaixo.
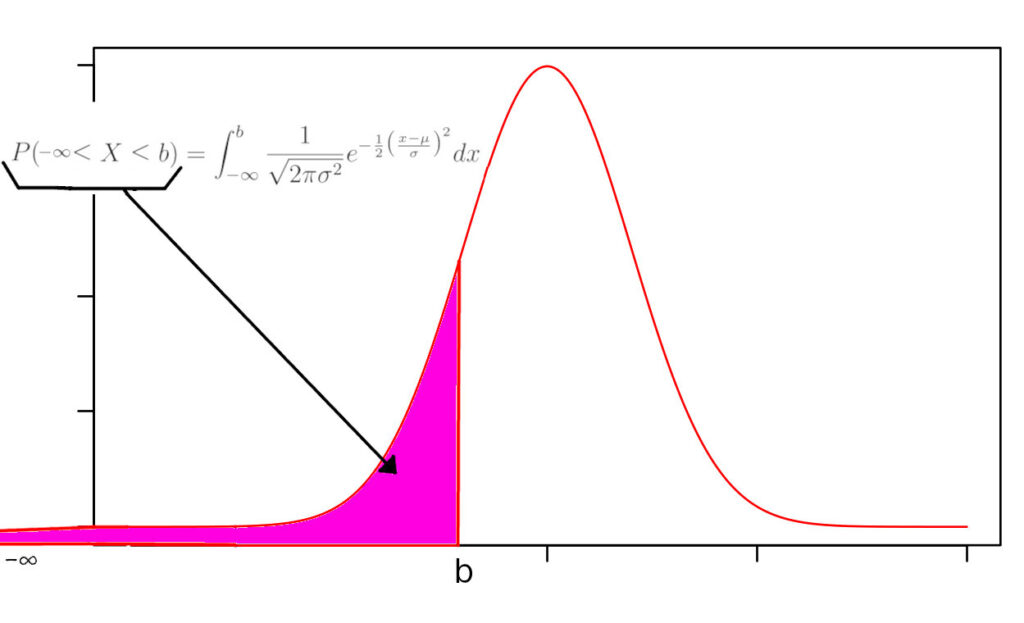
Assim, se você quer encontrar a probabilidade \(P\) tal que
\(P(a < X < b)\)
Você deve calcular:
\(P(a < X < b) = \int\limits_{-\infty}^b {{\frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ – \frac{1}{2}\big(\frac{{x – \mu}}{\sigma}\big)^2}}}dx – \int\limits_{-\infty}^a {{\frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ – \frac{1}{2}\big(\frac{{x – \mu}}{\sigma}\big)^2}}}dx \,\,\,\,\ a<b\)
Não entre em pânico. Na maioria das planilhas eletrônicas você consegue calcular a bruxaria acima fazendo a subtração dos resultados da função DIST.NORM.N
Dê uma olhada na tabela abaixo.
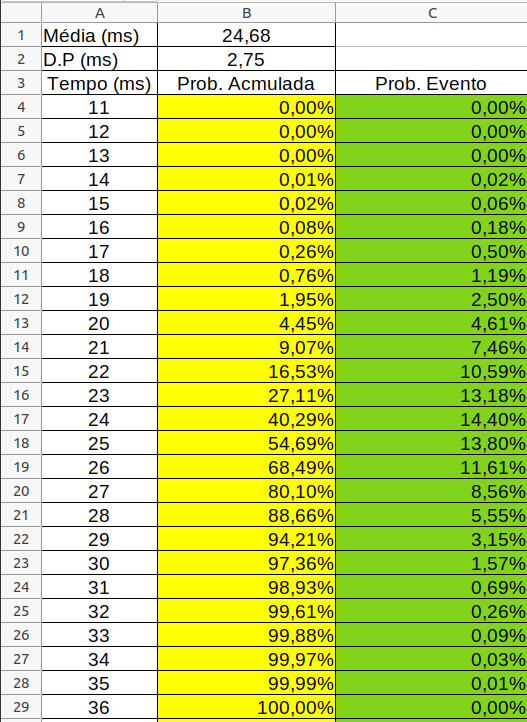
Na coluna B, nas linhas em amarelo, você coloca a seguinte fórmula:
DIST.NORM.N(tempo;media;desvio padrão;1)
O tempo é o valor da célula da coluna A adjacente; média é o conteúdo de B1; desvio padrão, B2; o valor 1 no final significa que a função vai retornar a probabilidade acumulada.
Por exemplo, para o tempo de 25ms (célula B18), a fórmula é:
DIST.NORM.N(A18;$B$1;$B$2;1)
Na coluna C, nas células em verde, para calcular a probabilidade de que o retardo, por exemplo, possa ser encaixado no tempo 12ms, você deve subtrair da probabilidade acumulada do tempo 13ms da acumulada de 12ms. Lembre-se que para que um retardo seja considerado como 12ms, no nosso exemplo, seu tempo deve estar entre 12,000ms a 12,99999…ms.
Veja que os resultados da planilha eletrônica são quase idênticos aos obtidos pela simulação. A simulação poderia ter sido feita na planilha. Mas eu, e isso é uma posição particular minha, prefiro construir códigos em C/C++ quando trabalho com sistemas de otimização, busca e simulações Monte Carlo. Nada impede que você faça em Excel, Libre Office etc. Mas lembre-se que isso terá um custo, dificilmente você conseguirá simular 10 milhões de retardos em uma planilha sem recorrer a macros. Outra opção, se você tem arrepios quando enxerga um código C ou similar, é utilizar algum SAC, como Matlab, Octave, Origin etc ou mesmo alguma linguagem interpretada que encapsula a maioria da complexidade, como Python e R, por exemplo.
Depois deste primeiro contato com a incerteza, podemos construir um modelo estatístico para uma sequência de detonação. Isso implica que você deverá olhar para o sequenciamento com outros olhos. Não como algo determinístico e certo, mas como uma sequência de eventos aleatórios que você deve, de certa forma, controlar.
A figura abaixo mostra o sequenciamento mais simples que podemos imaginar até agora. Dois furos que são iniciados no mesmo instante, mas que como você verá, não detonam no mesmo instante apesar de serem iniciados no mesmo instante. Se você entender essa frase seus projetos de sequenciamento nunca mais serão os mesmos.
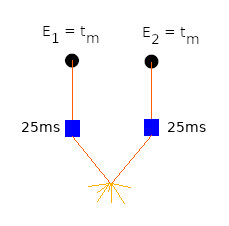
O valor esperado, tanto do furo 1, \(E_1\), quanto do furo 2, \(E_2\), é o valor médio (\(t_m\)) do retardo. Sabendo que os dois retardos possuem a mesma distribuição, podemos perguntar qual é a probabilidade dos dois retardos detonarem ao mesmo tempo? E aqui precisamos definir o que é “mesmo tempo”. Vamos supor que vamos medindo o instante exato que cada retardo detona. Tabelamos os valores da seguinte maneira:
\(t_{rn} = int(|t_1 – t_2|)\)
O valor \(t_{rn}\) é a diferença de tempo da n-ésima medição. Veja que guardamos apenas a parte inteira do número. Assim, um número como \(-0,67468\) será representando como apenas \(0\). Desta forma, consideramos que dois retardos detonam no mesmo tempo quando a parte inteira da sua diferença é zero. Logo, a nossa definição entende uma detonação simultânea quando a diferença entre dois retardos está no intervalo:
\(-0,99999999… \leq t_{rn} \leq 0,99999999…\)
Qualquer valor da diferença que esteja neste intervalo será considerado “instantâneo”.
Vamos agora simular 10 milhões de diferenças de tempo. Eu modifiquei um pouco o primeiro programa. Adicionei novas funcionalidades, dê uma olhada:
#include <stdio.h>
#include <math.h>
#include <unistd.h>
#include <gsl/gsl_cdf.h> // funçoes de dsitribuição de probabilidade
#include <gsl/gsl_rng.h> // geração de números aleaorios
int simulacoes = 0;
int detonadores = 0;
double media = 0.0f;
double dp = 0.0f;
double limite_inferior = 0.00;
double limite_superior = 0.00;
const gsl_rng_type *T;
gsl_rng *r;
double* TemposSorteados;
int encontrados = 0;
void LibertemAMemoriaJa()
{
free(TemposSorteados);
// liberando a memória alocada por gsl_rng_alloc
gsl_rng_free(r);
}
void CriarArrayTempos()
{
if(detonadores >= 0)
TemposSorteados = (double*)(malloc(detonadores * sizeof(double)));
else
TemposSorteados = NULL;
}
void SetupGSL()
{
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc(T);
}
double TempoRetardo(const double media, const double sd)
{
double u = gsl_rng_uniform(r); // numero aleatorio entre 0.000 e 1.000
double x = gsl_cdf_ugaussian_Pinv(u); // retorna um numero dentro de uma distribuição normal padrão N(0,1)
return x * sd + media;
}
void PreencheTempos()
{
for(int i = 0; i < detonadores; i++)
TemposSorteados[i] = TempoRetardo(media, dp);
}
int CalculaDiferencas()
{
int diferenca = 0;
for(int i = 0; i < detonadores; i++)
for(int j = i + 1; j < detonadores; j++)
{
diferenca = trunc((TemposSorteados[i] - TemposSorteados[j]));
diferenca = abs(diferenca);
if( diferenca > limite_superior || diferenca < limite_inferior)
return 0;
}
return 1;
}
void ValoresEntrada(int argc, char **argv)
{
char ch;
while( (ch = getopt(argc, argv, "s:d:m:p:a:b:")) != EOF )
{
switch(ch)
{
// numero de simulações
case 's':
simulacoes = atoi(optarg);
break;
// numero de detonadores
case 'd':
detonadores = atoi(optarg);
break;
// media
case 'm':
media = atof(optarg);
break;
// desvio padrao
case 'p':
dp = atof(optarg);
break;
// limite inferior
case 'a':
limite_inferior = trunc(atof(optarg));
break;
// limite superior
case 'b':
limite_superior = trunc(atof(optarg));
break;
}
}
}
int main (int argc, char ** argv)
{
SetupGSL();
ValoresEntrada(argc,argv);
CriarArrayTempos();
double porc = 0.00;
int contagem = 0;
//iteracao das simulacoes
for(int i = 0; i < simulacoes; i++)
{
PreencheTempos(media,dp);
if(CalculaDiferencas())
contagem++;
}
if(simulacoes > 0)
porc = (double)contagem / simulacoes;
porc *= 100.00;
printf("%d : %0.5f%%\n", contagem, porc);
LibertemAMemoriaJa();
return 0;
}Este programa aceita os argumentos:
s – número de simulações;
d – quantidade de detonadores;
m – média;
p – desvio padrão;
a – limite inferior;
b – limite superior;
O executável com os argumentos -s10000000 -d2 -m24.676 -p2.75 -a0 -b0 produz a saída 20.28069%.
Isto significa que, simulando 10 milhões de vezes a diferença de dois retardos de 25ms iniciados ao mesmo tempo, com um média de 24,676ms e desvio padrão de 2,75ms, em 20,29% da vezes a diferença inteira entre eles foi de 0ms.
Você pode verificar o resultado desta simulação Monte Carlo na sua planilha. Para isso, precisamos construir um sistema equivalente a dois retardos. O valor esperado da diferença de tempos dos retardos é:
\(E[t_{r}] = |E[t{r1}]-E[t_{r2}]| = 0ms\)
Como são eventos independentes, ou seja, o tempo de retardo de cada um não depende do tempo de retardo do outro, mas apenas das incertezas relacionadas aos erros do próprio dispositivo, a variância deste sistema é:
\(V[t_{r}] = V[t{r1}] + V[t_{r2}] = 2,75^2 + 2,75^2 = 15,125(ms)^2\)
E o desvio padrão:
\(\sigma = \sqrt{15,125(ms)^2} = 3,88908729652601ms\)
A diferença de tempo de detonação dos dois retardos de 25ms do nosso exemplo forma uma Normal com média 0ms e desvio padrão de 3,89ms. Com estes dados você pode construir uma tabela com o uso de DIST.NORM.N. Veja na figura abaixo.
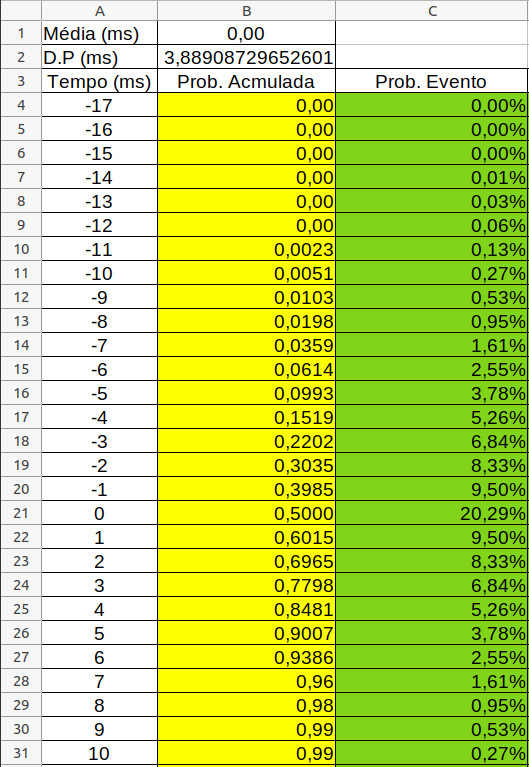
Nas células amarelas temos a fórmula
DIST.NORM.N(tempo;média;desvio padrão;1)
Já para a células verdes temos as seguintes situações:
a) Na célula correspondente ao 0ms, temos a fórmula B22 – B21. Isto significa que estamos aplicando a definição \(P(a < X < b)\) considerando que a probabilidade do valor “0ms” corresponde a área entre os valores -0,999999ms a 0,99999ms.
b) Já para a células correspondentes aos tempo menores que 0ms, devemos lembrar que, por exemplo, uma diferença de -1ms corresponde a valores entre -1,000ms e -1,9999ms, desta forma para o valor de -1ms devemos efetuar B20-B19 e assim sucessivamente.
Para as diferenças positivas, por exemplo, para 1ms, devemos fazer B23-B22 e assim sucessivamente.
Veja que a probabilidade associada a 0ms da planilha está muito próxima daquela obtida pela simulação.
Se queremos saber qual a probabilidade de detonarem com um módulo da diferença no intervalo de 8,000 a 8,99999ms podemos simular com os parâmetros
-s10000000 -d2 -m24.676 -p2.75 -a8 -b8
A minha simulação produziu uma saída de 1,90577%. Na planilha, se você somar os valores das células correspondentes as diferenças de 8m e -8ms vai encontrar um valor de 1,90241%. Muito próximo ao valor da simulação.
A tabela abaixo mostra os valores que encontrei tanto na planilha quanto na simulação Monte Carlo. Lembre-se que você não deve ler a coluna Diferença 8, por exemplo, como a probabilidade de dois retardos detonarem com diferença de exatamente 8ms entre eles, mas com uma diferença no intervalo de -8.000…ms a -8.99999…ms OU 8.0000…ms a 8.9999…ms.
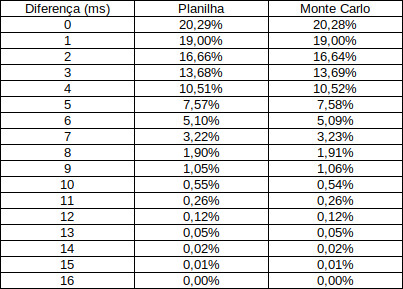
Um detalhe que não posso deixar de mencionar é que não tem como saber qual o retardo, da direita ou da esquerda, vai detonar primeiro. Quando os dois possuem um valor de diferença outro que 0ms, existe uma chance de 50% para cada um de ser o primeiro. É o estilo desmonte de rocha de jogar uma moeda.
Agora se queremos saber como se comportam uma série de retardos iniciados ao mesmo tempo, a coisa fica um pouquinho mais complicada.
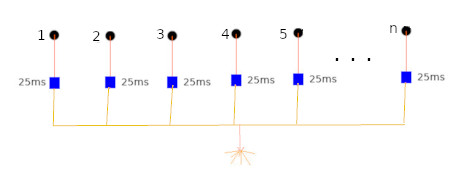
A probabilidade de todos os retardos detonarem exatamente ao mesmo tempo é virtualmente zero. Veja, para se calcular a probabilidade através da integral
\(P(a < X < b) = \int\limits_{a}^b {{\frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ – \frac{1}{2}\big(\frac{{x – \mu}}{\sigma}\big)^2}}}dx\)
para um ponto \(a=b\), teríamos que calcular a área de um segmento de reta, o que não faz sentido. Existem modos de impor um limite de forma que poderíamos tentar algo como:
\(P(X) = \lim\limits_{\epsilon\rightarrow 0}\int\limits_{a}^{a+\epsilon} {{\frac{1}{{\sqrt {2\pi \sigma^2} }}e^{ – \frac{1}{2}\big(\frac{{x – \mu}}{\sigma}\big)^2}}}dx\)
Mas acho que foge muito do foco aqui além de ser extremamente trabalhoso e difícil. Podemos conviver harmoniosamente com o intervalo (a,b) com \(a < b\).
Voltando a figura. Vamos simular a detonação de 2 a 100 retardos de 25ms iniciados de uma só vez e contar quantas vezes a subtração entre eles fica na casa do “0ms”. Resumindo, vamos calcular
\(int(|t_1 – t_2|)\)
\(int(|t_1 – t_3|)\)
\(int(|t_1 – t_4|)\)
\(\vdots\)
\(int(|t_1 – t_n|)\)
\(int(|t_2 – t_3|)\)
\(\vdots\)
\(int(|t_2 – t_n|)\)
\(int(|t_{n-1} – t_n|)\)
Veja que a quantidade de subtrações, \(S\), que podemos ter com \(n\) retardos subtraídos dois a dois são
\(S=\frac{n!}{2!(n-2)!}\)
considerando que $|t_1 – t_2| = |t_2 – t_1|$.
A tabela abaixo mostra a compilação da simulação Monte Carlos da iniciação simultânea de 2 a 100 retardos de 25ms.
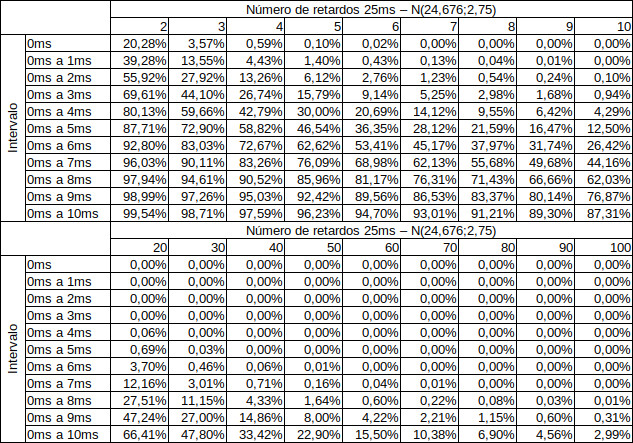
Perceba, sutilmente, que a tabela diz que a CME (Carga Máxima por Espera) também é uma variável aleatória para esta configuração de desmonte. Se você considera, como muitos livros e muita gente faz, que as cargas podem ser consideradas como “únicas” quando detonam com menos de \(8ms\) entre elas, então deve notar que, no nosso pequeno estudo teórico, a \(CME_8\) para 20 não-elétricos de \(25ms\) iniciados ao mesmo tempo tem \(\approx 27,5\%\) de chance de ocorrer. Assim, quando você soma as cargas de 20 furos nesta configuração e alimenta o seu modelo de regressão linear (que já não é lá muito bom) para previsão de vibrações, você faz o seu \(R^2\) diminuir devido a tristeza.
Para detonadores com tempo maior, assim como no filme do Homem Aranha, com um grande retardo vem uma grande dispersão. Como exemplo, vamos usar um não-elétrico de tempo nominal de \(3000ms\). A distribuição deste tempo de retardo poderia ser tranquilamente algo como \(N(2997,8;98,6)\). Dê uma olhadinha na figura abaixo.
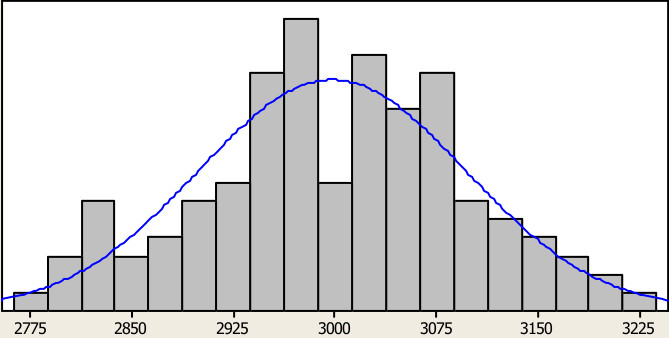
Da mesma maneira como fizemos com o 25ms, vamos simular este não-elétrico de 3000ms. Veja os resultados obtidos na tabela abaixo.
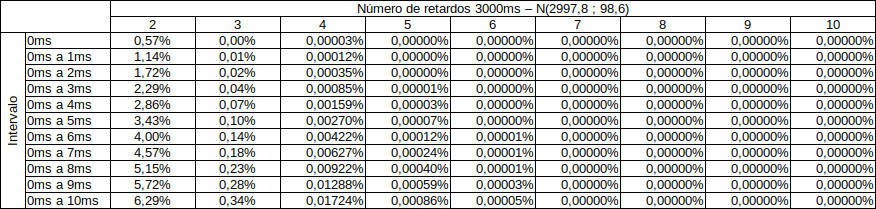
Percebeu? A chance de você detonar 2 não-elétricos de 3000ms com uma diferença de tempos entre eles de 0ms a 8ms é de 5,15%. Por exemplo, em sequencias de contorno para abertura de túneis é comum termos mais do que 10 não-elétricos de 3000ms sendo iniciados no mesmo instante. Neste caso, não só a CME é drasticamente alterada, mas também estamos tentando efetuar um smooth blasting (método mais comum) com cargas que não estão detonando no mesmo tempo. Queira você ou não, isso prejudica uma a obtenção de um corte legal. Existe uma técnica que desenvolvemos para eliminar esta dispersão nos furos de contorno, mas fica para outro texto.
Você pode estender a análise acima utilizando, por exemplo, uma distribuição binomial para calcular a probabilidade da CME devido a detonação de detonadores de dois em dois para um total de n detonadores. Ou 3 em 3, 4 em 4 etc. Isso vai te levar a responder a perguntas como “Qual a probabilidade de uma CME de Xkg se eu iniciar N não-elétricos no mesmo instante?”. Tenta aí.
Podemos calcular o tempo de retardo equivalente quando combinamos não-elétricos em um sequenciamento. Não basta somar apenas o valor nominal do não-elétrico e considerar que esta soma possui erro zero. Na verdade, dependendo da situação, isso pode ser perigoso. Você pode comprometer seriamente a sequência, causando sobreposições e “overlappings”. No restante do texto “overlapping” significa que uma sequência detonou antes que a sequência prévia tenha detonado.
A maneira mais simples de se construir um retardo equivalente é supor a sua normalidade e considerar o valor esperado como a soma ou subtração das médias e, conjuntamente, a soma das variâncias. Isso implica que o retardo equivalente dependerá de como se chega até ele com a sequência. Explico melhor. Veja as duas possibilidades de sequenciamento na figura abaixo. Ignorando as dispersões, ela são as mesmas. Mas uma delas possui uma desvantagem muito maior que a outra.
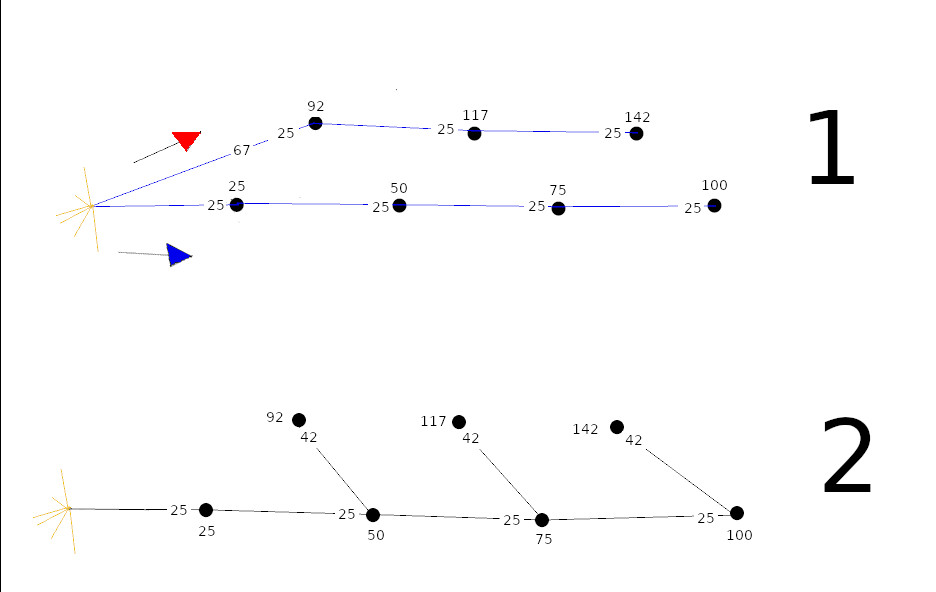
Suponha que todos os furos estão com uma escorva de não-elétrico de 250ms. Desta forma, os furos #3 (142ms) da segunda linha e o furo #4 (100ms) da primeira linha da sequência 1 podem ter seu retardo equivalente calculado como:
E[f_{2-3}] = t_{250} + t_{67} + t_{25} + t_{25} + t_{25}
V[f_{2-3}] = V_{250} + V_{67} + V_{25} + V_{25} + V_{25}
E[f_{1-4}] = t_{250} + t_{25} + t_{25} + t_{25} + t_{25}
V[f_{1-4}] = V_{250} + V_{25} + V_{25} + V_{25} + V_{25}
Suponha que os retardos podem ser representados por:
\(t_{25} = N(24,676 ; 2,75)
\\
t_{42} = N(42,331 ; 3,65)
\\
t_{67} = N(66,773 ; 4,43)
\\
t_{250} = N(250,32 ; 7,41)\)
Então
\(E[f_{2-3}] = 250,32 + 66,773 + 24,676 + 24,676 + 24,676 = 391,121ms
\\
V[f_{2-3}] = 7,41^2 + 4,43^2 + 2,75^2 + 2,75^2 + 2,75^2 = 97,220(ms)^2
\\
\sigma_{2-3} = \sqrt{97,220} = 9,86ms
\\
N_{2-3}(391,121;9,86)\)
Da mesma forma
\(N_{1-4}(349,024;9,22)\)
Perceba que na situação 1 que os caminhos para se chegar aos furos são independentes. Isso significa que a diferença de tempo entre os furos 1-4 e 2-3 são processos, também, independentes. Esperamos que a diferença de tempo entre eles seja
\(D_1 = 391,121 – 349,024 = 42,097ms\)
e
\(V_D1 = 9,86^2 + 9,22^2 = 182,3786(ms)^2 \rightarrow \sigma_D = 13,50476ms\)
A probabilidade do tempo de retardo entre estes dois furos pode então ser representada por uma normal \(N(42,097; 13,50476)\). Vamos perguntar para esta distribuição qual a chance da sequência 1 ser invertida? Ou seja, qual a chance do furo da linha 2 detonar antes do furo da linha 1.
Para responder podemos simular uma Monte Carlo, utilizar a definição de FDP ou mesmo a tabela de z-score, observando que essa pergunta é equivalente a \(P(X < 0)\). Na simulação obtemos 0,08983%. Pelo calculo através do z-score temos:
\(z = \frac{0 – 42,097}{13,50476} = -3,12\)
Procurando em una tabela de z-score o valor de -3,12 você vai encontrar um valor de 0,0009 ou 0,09%. Valor próximo ao da nossa simulação.
Agora vejamos a situação do caminho 2. A simulação retorna a probabilidade de overlapping em 0,00694%. A diferença de tempos entre os furos depende somente da dispersão de 3 peças: fundo do furo 1-4, fundo do furo 2-3 e do retardo de 42ms, pois o caminho para chegar até eles é compartilhado. Podemos dizer que ambos possuem um passado em comum. A normal associada a diferença de tempo entre os dois furos nesta nova configuração é
\(D_2(42,331; 11,09678)\)
Da mesma maneira, a probabilidade de overlapping é:
\(z = \frac{0 – 42,331}{11,09678} = -3,82 \rightarrow P(x < 0) = 0,007\%\)
Veja que a variância da sequência 2 para a diferença de tempo dos dois furos depende apenas dos três detonadores associados à eles. Já na sequencia 1, a variância depende de quantos retardos temos até se chegar aos furos. Isso significa que a probabilidade de overlapping depende do passado de ambos, ou seja, de quantos retardos detonaram. Vejamos, imagine que temos não 3, mas 30 retardos de 25ms até se chegar ao furo 1-30 e 29 retardos de 25ms mais um retardo de 67ms até se chegar ao furo 2-29. A normal que representa a diferença entre estes dois furos será
\(D(42,097; 23,992)\).
O desvio padrão é muito maior, isso na prática significa que a probabilidade de overlapping agora é:
\(z = \frac{0 – 42,097}{23,992} = -1,75 \rightarrow P(x < 0) = 4,01\%\)
Exatamente isso. Se você adotar uma ligação com caminhos independentes, você terá 4% de chance de overlapping neste exemplo. Enquanto que se adotar uma ligação com passado comum, por exemplo, sua chance de overlapping permanecera em 0,007%.
E a probabilidade de overlapping aumenta muito se você não tiver cuidado na escolha dos tempos. Já ouvi falar de desmontes onde se utilizava 1000ms de fundo e 17ms na superfície e 4000ms no fundo e 42ms na superfície. Para esta combinação de tempos nem precisamos ir muito longe para verificar onde está o problema. Vejamos:
\(N_{17}(16,898; 2,03)
\\
N_{42}(42,331 ; 3,65)
\\
N_{1000}(1043,5; 36,0)
\\
N_{4000}(3982,9; 112,3)\)
A figura abaixo mostra configuração de dois furos sequenciados com 1000ms/17ms.
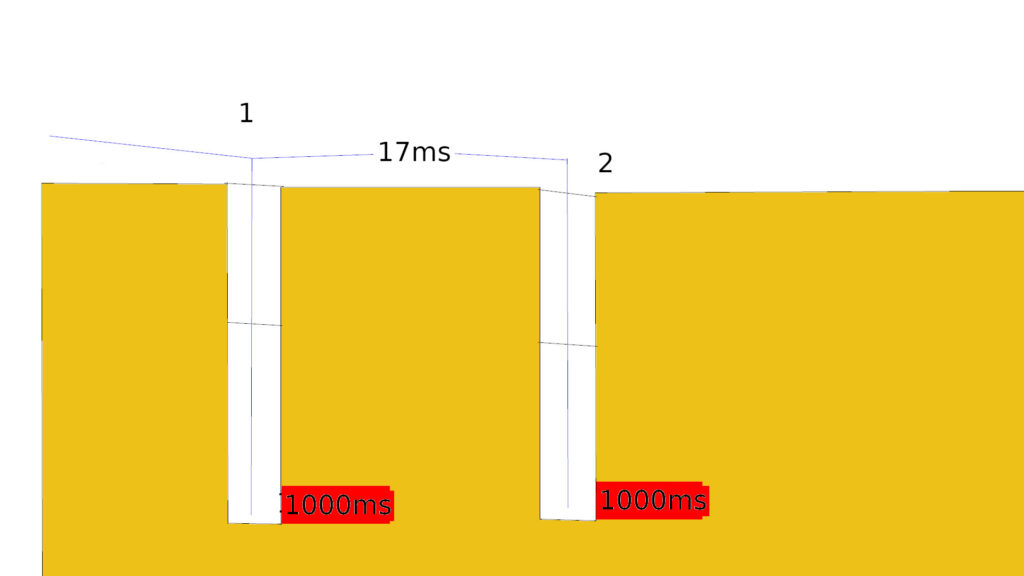
A normal associada à diferença de tempo desta situação é
\(D(16,898; 50,952)\)
e a probabilidade de overlapping é:
\(z = \frac{0 – 16,898}{50.952} = -0,332 \rightarrow P(x < 0) \approx 37\%\)
Você não leu errado. A probabilidade é de 37%. Na minha humilde opinião, um risco inaceitável.
A configuração mostrada na figura abaixo não é muito diferente.
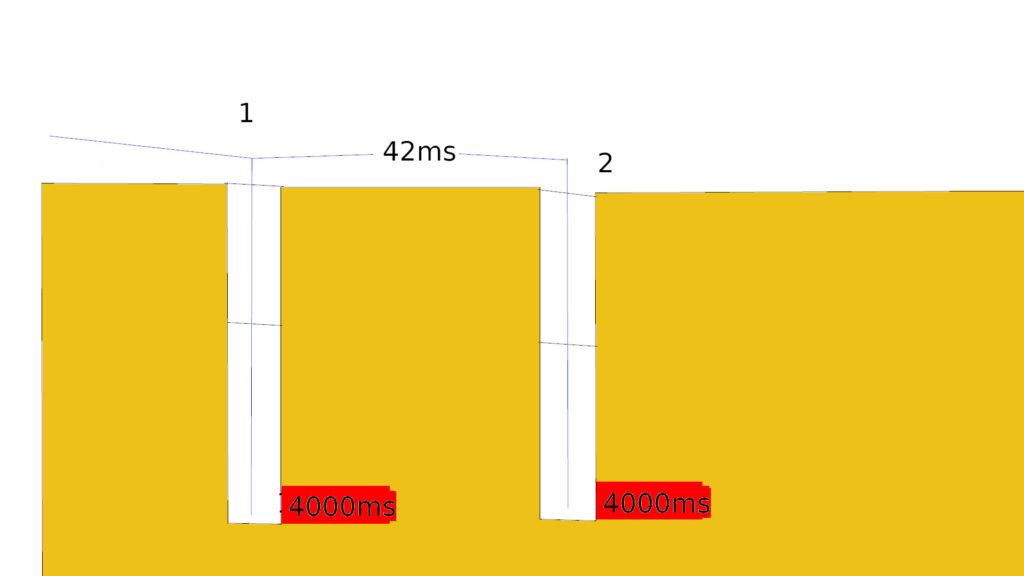
\(D(42,331; 158,85)
\\
z = \frac{0 – 42,331}{112,36} = -0,27 \rightarrow P(x < 0) \approx 39\%\)
As simulações Monte Carlo feitas para ambas as configurações resultaram em 37,02619% e 39,47958%.
Ignorar as dispersões pode ser um erro gave no seu projeto. Fique atento. Futuramente, em outro texto, vou te mostrar como construir um cronômetro com menos de US$150,00 para medir a dispersão de não-elétricos.
A análise estatística feita aqui não trata do assunto exaustivamente. Simplifiquei e resumi muita coisa, até porque se assim não fosse, o texto ficaria muito longo e, talvez, tedioso para além do que já é. Mas é um passo inicial para você começar, se assim quiser. Os vídeos abaixo mostram situações onde análises estatísticas foram usadas para obter um controle melhor das vibrações. Espero que goste.

Congrats!!!
Muito bom Golin. Essa abordagem da função de probabilidade dos tempos considerando uma distribuição normal dessa variação muito interessante e com isso a carga por espera associada. Excelente texto